bardzo prosze o pomoc mezzo: x−1< √7−x Rozwiaz nierownosc

daras: x ≤ 7 i podnieś do kwadratu a dalej r−nie kwadratowe+spr dziedziny na koniec

Kacper: Nie można podnosić nierówności stronami bez odpowiednich założeń.

ZKS:

:): x−1<√7−x || ² (x−1)²<|7−x| x²−2x+1<7−x ∨ x²−2x+1>−7+x x²−x−6<0 x²−3x+8>0 Δ=1+24=25 Δ<0 brak pierwiastkow √Δ=5 x₁=−2 x₂=3 x∊(−2,3)

ZKS: Źle.

Kacper: ZKS dawno cię nie było

daras: ale x−1 −√7−x < 0 chyba można

ZKS: Też nie. Przykładowo dla x = −2 otrzymasz coś takiego −2 − 1 − √7 − (−2) < 0 −3 − 3 < 0 −6 < 0 jest prawdą podnosząc do kwadratu dostaniemy 36 < 0.

ZKS: Jakoś tak wyszło, że dawno tu zaglądałem ostatnio.

Kacper: Przenosić zawsze wolno, tylko tak jak pokazał ZKS nie zawsze można podnosić do kwadratu

ZKS: Według mnie najlepiej będzie zrobić w następujący sposób. Dla x ≤ 7 zachodzi x − 1 = −|7 − x| + 6 = −√(7 − x)² + 6 można wtedy dla ułatwienia zrobić podstawienie u = √7 − x i dostaniemy nierówność kwadratową ze zmienną u. −u² + 6 = u

daras: (3;7]

ZKS: Rozwiązaniem jest x ∊ (−∞ ; 3).

daras: tak wychodzi z tych Twoich podstawień ale graficznie to 3 < x ≤ 7

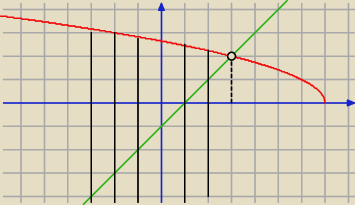
ZKS: Graficznie też wychodzi.

daras: sorry , masz dobrze..cały czas rozwiązywałem odwrotną nierówność x < 3

ZKS:

Mila: 1) dla x≤7 i x<1 nierówność jest spełniona dla każdego x, lewa strona ujemna − prawa dodatnia. 2) x−1≥0 ⇔x≥1 dla x≥1 i x≤7 obie strony dodatnie; (x−1)²<7−x x²−2x+1−7+x<0 x²−x−6<0 i x∊<1,7> Δ=25 x=−2 lub x=3 x∊<1,3) =========== x∊(−∞,3)