analityczna kasia: wyznacz miarę kąta ostrego między prostymi k il k:x−8=0 l:x−y−200=0 wiem jaki jest wzór ale nie wiem co zrobic, bo w k nie ma y

J: k − prosta: x = 8 (równoległa do osi OY)

kasia: tyle wiem, ale jak obliczyć ten kąt?

J: . a jaki kąt z osią OX tworzy prosta l ..?

kasia: no 45 stopni, ale nie rozumiem dlaczego skoro pierwsza prosta jest równoległa do oy to szukamy kąta tehj drugiej z osią ox

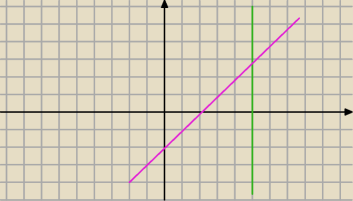
J: ...jaki kąt tworzą te proste ze sobą ...?

5-latek: Witaj J Nie wiem czy ja dobrze mysle ale skoro te proste nie sa do siebie prostopadle to ten wzor na kat miedzy prostymi dziala w tym przypadku

J: Cześć.. ...., a co wstawisz do wzoru jako wspólczynnik kierunkowy prostej: x = 8

5-latek: a₁=0

J: ... w tym przypadku zadziała, ale np: a₁ = √3 a₂ = 0 ,

	√3
wtedy: tgβ = I		I = √3 (60o),a proste tworzą kąt 30o
	1

J: .... i jeszcze..... prosta: y = 0*x + k .... jest równoległa do osi OX, a nie prostopadła ...

5-latek: No tak . Bede w takim razie musial jescze doczytac

5-latek: Mam geometrie analityczna Starka wiec zajrze do niej pozniej

5-latek: Zalazlem ale w innej jesli mamy prosta x=a i prosta y=mx+b to kąt jakie tworza te proste = 90 stpni gdy m=0

	1
Natomiast gdy m nie jest rowny 0 to kat wynosi tgx=+/−
	m

J: ... a wiesz skąd taki wzór...?

5-latek: Szczerze powiem nie bardzo .

J:

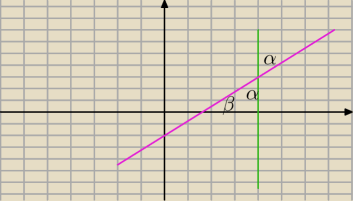
	1		1
m = tgβ ... tgα = tg(90−β) = ctgβ =		=
	tgβ		m

5-latek: Az mnie zatkalo Wzory redukcyjne . A ja chcialem juz sobie przypominac cosinus i sinus kąta miedzy prostymi bo cos tak mi sie przypominalo A tak swoja droga to ciekawe ilu licealistow wie dlaczego tak jest

J: ...

Bogdan: prosta k₁: y = a₁x + b₁ albo A₁x + B₁y + C₁ = 0 prosta k₃: y = a₂x + b₂ albo A₂x + B₂y + C₂ = 0 a₁ ≠ a₂ α − miara kąta między prostymi k₁ i k₂

	a1 − a2		A1B2 − A2B1
tgα = |		| albo tgα = |		|
	1 + a1a2		A1A2 + B1B2