wykres
Kamil:
A jak narysować takie coś
|sin(x)|+sin(x)
1. sin(x)<0
−sin(x)+sin(x)=0
2.sin(x)≥1
sin(x)+sin(x)=2sin(x) ?
16 paź 00:45
PW: Tak, "kawałkami" jest to funkcja stała o wartości 0, a "kawałkami" 2sinx. Wyznaczyć te kawałki
osi i można rysować.
W 2. masz literówkę: powinno być sinx ≥ 0.
16 paź 00:50
Kamil:
Właśnie ale ja takie kawałki odpowiednio umieścić ?
16 paź 00:51
Kamil:
?
16 paź 00:57
PW: Po prostu rozwiązać nierówność sinx≥0 − otrzymasz te x, dla których f(x) = 2sinx.
16 paź 00:58
Kamil:
dziękuję
16 paź 00:59
Eta:
16 paź 01:08
Kamil:
A mogła by Pani wytłumaczyć ? Wiem, że już późno, ale może coś da się zrobić. ?
16 paź 01:09
Eta:
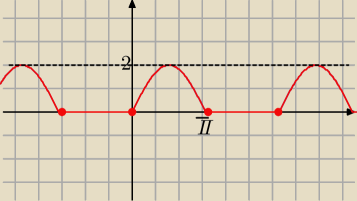
sinx≥0 w przedziałach (0+2kπ,π+2kπ)
zatem w tych przedziałach
f(x)=|sinx|+sinx= sinx+sinx= 2sinx ( rysujesz wykres y=2sinx tylko w tych przedziałach
sinx<0 ⇔x∊(π+2kπ,2π+2kπ)
y= −sinx+sinx=0 to y=0 −−−funkcja stała w tych przedziałach (rysujesz jak na moim rys
16 paź 01:21
Kamil:
Dziękuję już mam jakiś punkt odniesienia.
16 paź 01:25
Eta:

16 paź 01:32
Kamil:
czy koniecznie trzeba rozwiązać nierówność żeby to namalować ?
16 paź 14:36
PW: Oj tam, wielkie rozwiązywanie. Przecież wiesz, gdzie sinus dodatni (nawet o 0:50 pisałem
"wyznaczyć te kawałki osi" sugerując tym samym, że to coś oczywistego).
16 paź 16:41

