Wzajemne położenie dwóch okręgów Code::Blak: Podaj liczbę punktów wspólnych okręgu opisanego podanym równaniem z okręgiem o środku S (1,3) i promieniu r w zależności od tego promienia. x2 + y2 + 4x + 2y + 1 = 0 To wychodzi że : O ( −2 , −1 ) r = 4 |OS| = 5 i co dalej bo tego nie kumam

Kacper: Popraw treść, bo na pewno nie była taka jak piszesz.

Code::Blak: Podaj liczbę punktów wspólnych okręgu opisanego podanym równaniem z okręgiem o środku S( 1, 3) i promieniu r w zależności od tego promienia. a) x² + y² + 4x + 2y + 1 = 0 Moje obliczenia : O ( −2 , −1 ) r = 4 |OS| = 5

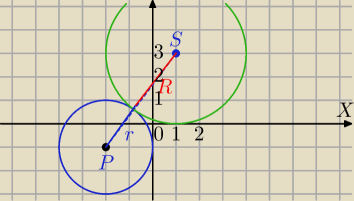
Mila: S (1,3) x² + y² + 4x + 2y + 1 = 0⇔ (x+2)²−4+(y+1)²−1+1=0⇔ (x+2)²+(y+1)²=4 , r²=4⇔r=2, P=(−2,−1) |PS|=√(1+2)²+(3+1)²=√9+16=5 R=5−2=3 okręgi styczne zewnętrznie− jeden punkt wspólny dalej sam?

Code::Blak: no właśnie tej dalszej części nie rozumiem

Mila: Weź cyrkiel i narysuj okrąg o śodku S i o promieniu R=4 R=6 R=5+2=7 R=8 Odpowiedz, jak narysujesz to zrozumiesz.

Code::Blak: Nie rozumiem

Code::Blak: w od coś jest ala 0 dla (0,3) ∪ ( 7 , ∞) 1dla {3,7} 2 dla (3,7)

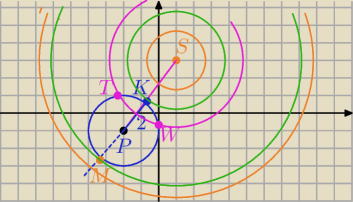
Mila: Jednak nie rysowałeś, dałam takie promienie, abys to zauważył. 1) jeżeli 0<R<3 to brak punktów wspólnych, okręgi nie przetną się SM=5+2=7 Jeżeli R>7, to okręgi też nie przetną się 2) SK=3 Jeżeli R=3 to okręgi mają jeden punkt wsólny K, są styczne zewnętrznie Jeżeli R=SM=7, to okręgi mają jeden punkt wspólny M, są styczne wewnętrznie. 3) Jeżeli 3<R<7 to masz dwa punkty przecięcia

Mila: https://matematykaszkolna.pl/strona/473.html

E: Może wypadałoby podziękować?