Wzajemne położenie dwóch prostych Code::Blak: Dany jest okrąg o środku O (−1,2) i promieniu 2. Określ wzajemne położenie tego okręgu oraz okręgu o środku S i promieniu r OK 1. O(−1,2) r₁=2 |OS| = 2.5 r₂=4,5 Styczne zew. |OS| = r₂ + r₁ 2,5 = 4,5 + 2 ( nope) wew. |OS| = | r₁ − r₂| >0 2,5 = | 4,5 − 2 | 2,5 = 2,5 >0 Tak to ma być ?

Code::Blak: |OS| = 2,5 r = 4,5

5-latek: Proponuje CI jeszce raz przeczytac na glos tresc twojego zadania

Code::Blak: no takie mam w podręczniku a ten drugi post to jest uzupełnienie do zadania

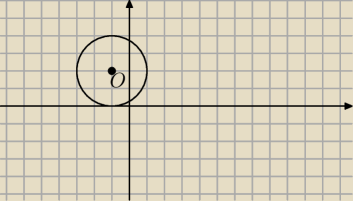
5-latek: Masz narysowqany okrag o srodku O(−1,2) i promieniu 2 Teraz jak mamy okreslic wajejmne polozenie tego okregu wobec okregu o srodku S i promieniu r jesli nie mamy nic powiedzianie na temat tego drugiego okregu Proponuje napisac cala tresc zadania a nie wybierac jego fragmenty

Code::Blak: Naprawdę to jest całą treść. mogę się z tobą z kontaktować jak mi nie wierzysz

Code::Blak: cała*

5-latek: Powiem CI tak . jesli to jest cala tresc zadania to ja sie poddaje https://matematykaszkolna.pl/strona/473.html Tak sie okresla wzajemne polozenie dwoch okregow ale trzeba jeszce miec do tego drugi okrag

Code::Blak: może spróbuj zrozumieć z moich zapisków

Code::Blak: albo podam ci jak pierwszy przykład wyglądał

5-latek: Poprosilem innego kolege zeby tu spojrzal

Bogdan: r₁ = 2; r₂ = 4,5; |OS| = 2,5 |r₁ − r₂| = 2,5 = |OS| okręgi są wewnętrznie styczne