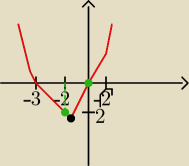
... tom: Dana jest funkcja f(x)= x² + 3x: a) wyznacz najmniejszą i największa wartość funkcji w przedziale <−2, √2> A więc tak: f(x)= x² + 3x a= 1, b=3, c= 0 Δ=9 x1= −3, x2= 0 p= −1,5, q= −2 więc z tego rysunku powyżej wynika, że y min= −2 a y max= 0 Może ktoś sprawdzić czy dobrze zrobiłem zadanie

Nikka: największą wartość ma raczej dla x=√2

Mażena: Najmniejszą wartość funkcja kwadratowa przyjmuje w q wierzchołka na który jest wzór

	Δ		9		1
q=−		, co w tym zadaniu wygląda następująco: q=−		=−2
	4a		4		4

co do wartości największej w danym przedziale to z wykresu widzimy że jest ona dla argumentu x=√2, który wstawiamy do wzoru funkcji i dostajemy: 2+3√2

tom: No tak najmniejsza wartość tego tej funkcji, co odczytamy z wierzchołka to 2¹₂, ale w przedziale <−2, √2> najmniejsza wartość będzie −2 tak mi się wydaje