Rozwiąż Równanie Daw.: |2−x| + |x+3| = 5 Rozwiąż równanie. Dziękuje

Kacper: |2−x|=|x−2| Suma odległości liczby od liczb −3 i 2 jest równa 5. Odp. x∊<−3,2>

olexy: ale dla jakiego x?

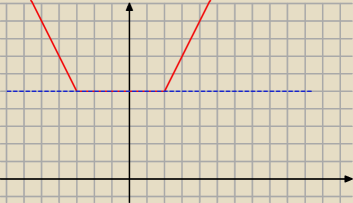
bezendu: |x−2|+|x+3|=5 nieskończenie wiele rozwiązań

Daw.: Tylko, że muszę przedstawić 3 warunki :c

5-latek: https://matematykaszkolna.pl/strona/1796.html

Daw.: 5−latek tylko, ze ja nie mam x−2 tylko 2−x

Kacper: Jakbyś umiał/a wytłumaczyć, to wystarczy to co ja napisałem

Kacper: Daw. pisałem przecież, że |2−x|=|x−2|

Daw.: Obawiam się Kacper, że chyba nie da rady

Daw.: Faktycznie, gapa ze mnie!

5-latek: Masz przyklad . Wiec wzoruj sie na tym przykladzie . To nie jest trudne Wiec pisz rozwiazanie tutaj .

PW: Znana jest nierówność |a + b| ≤ |a| + |b|, przy czym ciąg dalszy tego twierdzenia brzmi − a równość ma miejsce wtedy i tylko wtedy, gdy liczby a i b są jednakowych znaków. Biorąc a = 2−x i b=x+3 otrzymamy |2−x+x+3| ≤ |2−x| + |x+3| czyli 5 ≤ |2−x| + |x+3|. Po takim spostrzeżeniu widzimy, że zadanie polega na rozwiązaniu nierówności 5 ≤ |2−x| + |x+3| ≤ 5, to znaczy równości |2−x| + |x+3| = 5, ta zaś ma miejsce wtedy i tylko wtedy, gdy liczby 2−x oraz x+3 są jednakowych znaków. (2−x ≥ 0 ∧ x+ 3 ≥ 0) ⋁ (2−x < 0 x+ 3 < 0). Rozwiązaniem pierwszej koniunkcji są x ∊ (−3, 2), druga nie ma rozwiązań. Jest to mój ulubiony sposób rozwiązywania takich zadań − żadnego "rozbijania na przedziały", żadnych rysunków. Autor podpowiadał taką możliwość pisząc |2−x| zamiast zwyczajowego |x−2| Dokładna znajomość twierdzeń to podstawa.

PW: Sie wymądrzam, a rozwiązanie podałem bez krańców, powinno być x∊[−3, 2] oczywiście.

Kacper: PW jestem pełen podziwu twoim rozwiązaniom. Za to mogę się założyć, że autor nie to miał na myśli pisząc |2−x|. Chyba, że to ty byłbyś autorem