
 Dane są zbiory
A = (−∞; −2)∪<3;∞)
B = <−5;3>
Wyznacz zbiory A∩B, A−B.
Ile liczb w postaci k2 gdzie k jest liczbą całkowitą należy do zbioru B−A ?
Dane są zbiory
A = (−∞; −2)∪<3;∞)
B = <−5;3>
Wyznacz zbiory A∩B, A−B.
Ile liczb w postaci k2 gdzie k jest liczbą całkowitą należy do zbioru B−A ? 

 I ja sobie to narysowałam
i wyznaczyłam że A∩B = <−5;−2> ∪ {3}
A−B = (−∞;−5) ∪ (3; ∞)
B−A = <−2;3)
więc do zbioru B−A należy 5 liczb w postaci k2, gdzie k⊂C, bo są to −22 −12
02 12 22
proszę sprawdźcie czy to dobrze
I ja sobie to narysowałam
i wyznaczyłam że A∩B = <−5;−2> ∪ {3}
A−B = (−∞;−5) ∪ (3; ∞)
B−A = <−2;3)
więc do zbioru B−A należy 5 liczb w postaci k2, gdzie k⊂C, bo są to −22 −12
02 12 22
proszę sprawdźcie czy to dobrze 








 ?
?
| −4 | ||
a co z liczbą | należy? | |
| 2 |
| 1 | 1 | |||
Co do zbioru B−A to ja bym zaliczyll tylko | i | |||
| 2 | 2 |
| −2 | 0 | 2 | ||||
Dlaczego | = −1 , | =0 i to samo | =1 | |||
| 2 | 2 | 2 |
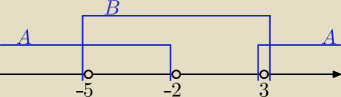 Proponuję konsekwentnie od lat taki sposób rysowania przedziałów liczbowych, rozwiązanie
widać moim zdaniem wyraźniej.
A∩B = <−5, 2)∪{3}
B \ A = <−2, 3)
Proponuję konsekwentnie od lat taki sposób rysowania przedziałów liczbowych, rozwiązanie
widać moim zdaniem wyraźniej.
A∩B = <−5, 2)∪{3}
B \ A = <−2, 3)
 Pewnie przy pisaniu A∩B=<−5,−2)U{3}
Pewnie przy pisaniu A∩B=<−5,−2)U{3}
 , oczywiście jest −2, co widać na rysunku, a nie 2, dziekuję
, oczywiście jest −2, co widać na rysunku, a nie 2, dziekuję