Geometria analityczna trq: Prosta równoległa do osi OY przecina okrąg (x+1)² + (y+3)² = 100 w punktach A i B. Wyznacz równanie tej prostej jeśli |AB| = 12. mam jeszcze takie techniczne pytanie. dlaczego przy wyrażeniu (−x−2)² nie mogę wyciągnąć minusa przed nawias?

J: ... możesz, ale ... (−x−2)² = [(−1)*(x+2)]² = (x+2)²

trq: okej, rozumiem. nadal jednak nie wiem jak rozwiązać pierwsze zadanie.

Kacper: prosta równoległa do osi OY ma równanie?

J: ...zrób szkic ... zobaczysz ,że łatwo wyznaczysz odległość tej prostej od środka okręgu... ... prosta ma równanie: x = a ( gdzie a , to ta odległość) .....

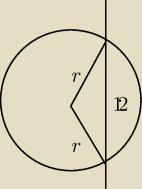
J: popatrz na rysunek ...

J: ..... oczywiście będą dwie proste .. x = x_s + a oraz x = x_s − a

trq: Jedyne co mi przychodzi do głowy przy wyznaczeniu odległości środka okręgu od prostej to skorzystanie z twierdzenia pitagorasa. Dobrze myślę?

J: Dokładnie...

trq: Okej, rozwiązałem. A co jeśli nie byłaby równoległa do żadnej osi?

J: ... byłoby trochę trudniej .... chyba ,ze autor dałby inne ułatwienie jak w tym zadaniu...