prawdopodobieństwo Blue: Udowodnij własność: P(AUB) = P(A) + P(B) − P(AnB) Bardzo bym prosiła o przedstawienie dowodu

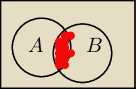
jakubs: Czerwone pole to jest A∩B. Tylko nie wiem czy tak można to dowodzić

jakubs: http://cieciura.net/mp/pdf/czesc6.pdf Strona 17 może coś pomoże.

Maslanek: Zapomniałem już jak się dowód przeprowadza tego faktu, ale trochę ta strona pomogła Prawdopodobieństwo jest funkcją przeliczalnie addytywną, więc jeżeli tylko A*B=∅, to P(A+B)=P(A)+P(B) Zatem A+B możemy zapisać w postaci A+(B\(A*B)). Wtedy A*(B\(A*B))=∅ Zatem P(A*(B\(A*B))=P(A)+P(B\(A*B)) (gwiazdka) Dodatkowo właśność, że jeżeli A⊂B, to P(B)≥P(A) Idąc z tej własności znów mamy, że P(Ω)=P(A+A')=P(A)+P(A') ⇔ P(A')=1−P(A) Dalej jeżeli A⊂B, to P(B)=P(A+(B\A))=P(A)+P(B\A), skąd P(B\A)=P(B)−P(A) No i korzystając z tego, że A*B⊂B mamy w końcu, że P(B\(A*B))=P(B)−P(A*B) Wtedy (gwiazdka) P(A+B)=P(A)+P(B)−P(A*B), co kończy dowód

Mila: Jeżeli mamy rozłączne zdarzenia C i D, to P(C∪D)=P(C)+P(D) Przedstawiamy A∪B jako sumę rozłącznych zbiorów, patrz ilustrację Jakubsa A∪B=(A\B)∪(A∩B)∪(B\A) P(A∪B)=P(A\B)+P(A∩B)+P(B\A) Spróbuj dokończyć.

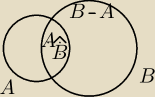
5-latek: Mamy nastepujace tozsamosci AUB=AU(B−A) B=(B−A)U(A∩B) Poniewaz A∩(B−A)=∅ (B−A)∩(A∩B)=∅mamy 1. P(AUB)= P(AU(B−A))= P(A)+P(B−A) 2. P(B)= P(B−A)U(A∩B))=P(B−A)+P(A∩B) Wyznaczajac P(B−A) z drugiego rownania i wstawiajac do 1 rownania otzrymamy P(AUB)=P(A)+P(B)−P(A∩B) cbdo

Blue: Mila : P(AUB) = P(A\B) + P(AnB) + P(B\A) P(AUB) = P(A) − P(AnB) +P(AnB) + P(B\A) P(AUB) = P(A) + P(B\A) P(AUB) = P(A) + P(B) − P(AnB) Może tak być?

Mila: Dobrze.

Blue: Dzięki wszystkim !