Najmniejsza i największa wartośc funkcji qwerty: Wyznacz najmniejszą i największą wartość funkcji f(x,y)=x−0,5y w obszarze wyznaczonym przez układ nierówności: −x+y ≤ 3 x+3y ≥ 13 x+y ≤ 9 Największa wartość wychodzi mi −1, a najmniejsza 6. W odpowiedziach jest odwrotnie. Proszę o pomoc

qwerty: ?

Kacper: pokaż rachunki

qwerty: Narysowałam obszar w układzie współrzędnych. Potem wyliczyłam współczynnik kierunkowy a=2 i poprowadziłam do niego proste równoległe. Najniżej oś OY przecinała prosta poprowadzona z wierzchołka określonego układem x+3y ≥ 13 x+y ≤ 9 Wyliczyłam współrzędne tego wierzchołka x=7, y=2 Najwyżej oś OY przecinała prosta poprowadzona z wierzchołka określonego układem −x+y ≤ 3 x+3y ≥ 13 Wyliczyłam współrzędne tego wierzchołka x=1, y=4

qwerty: ?

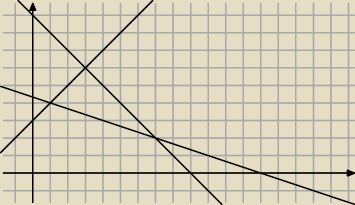
Kacper: Mamy trójkąt. I w nim szukamy wartości największej i najmniejszej.

qwerty: Tak wiem, ale tak jak już pisałam najniżej oś OY przecina prosta poprowadzona z wierzchołka (7,2), czyli wartość najmniejsza to 7−0,5*2=6, a ma wyjść −1

J: .... przecież największa wartość to: 6 ( 7 −0,5*2 = 6 ) i najmniejsza to: − 1 ( 1 − 0,5*4 = −1)

qwerty: Ale dlaczego? Ja mam odwrotnie, ponieważ wierzchołek, z którego jest poprowadzona prosta przecinająca oś OY ma współrzędne (7,2), więc to powinna być wartość najmniejsza (?)

Fizyk ale też matematyk: a mi sie policzylo 5

Fizyk ale też matematyk: wariactwo

Fizyk ale też matematyk: musialem liczyc od nowa

qwerty: Ktoś pomoże?

J: czy to rozumiesz , co masz zrobić w tym zadaniu ..? .... masz znaleźć najmniejszą i najwiekszą wartość funkcji dwóch zmiennych (x,y) określoną wzorem: f(x,y) = x − 0,5y w podanym obszarze ( trójkącie ).... ..... ta funkcja przyjmuje największą wartość w punkcie (7,2) równą 6 oraz najmniejszą w punkcie (1,4) równą −1

qwerty: Na lekcji nauczycielka pokazała sposób na rozwiązywanie tego typu zadań i 6 na 7 z zadanych zadań mi wyszło. Jedno, które nie wychodzi to właśnie to. Robię dokładnie tym samym sposobem, a wartości w tym przykładzie wychodzą odwrotne. Wytłumacz mi proszę, dlaczego największa wartość jest w punkcie (7,2) jeśli jest on położony najniżej w stosunku do innych wierzchołków tego trójkąta?

J: ..... przecież położenie wierzchołków nie ma tu znaczenia .... tylko przepis funkcji... ...... złóżmy ,ze przepis funkcji jest; f(x,y) = x + y ..... zauważ,że w tym trókącie wartość funkcji dla punktu (7,2) byłaby taka sama jak dla punktu (3,6) , a przecież te punkt (3,6 ) leży wyżej niż punkt (7,2)

qwerty: Na lekcji pani mówiła, żeby to rozwiązać w taki sposób: Obliczenie współczynnika kierunkowego (w tym zadaniu a=2), zaznaczenie go w układzie i poprowadzenie prostej przechodzącą przez a i przez punkt (0,0). Następnie należy poprowadzić proste równoległe do tej prostej. Prosta, która przecina oś najwyżej i najniżej będzie pokazywała, których wierzchołków należy użyć do obliczenia wartości najmniejszej i największej. W każdym zadaniu tego typu ten sposób się sprawdził, natomiast tu wychodzi odwrotnie i nie mogę zrozumieć dlaczego.

3Silnia&6: Sam to napisales: "Prosta, która przecina oś najwyżej i najniżej będzie pokazywała, których wierzchołków należy użyć do obliczenia wartości najmniejszej i największej." ...

qwerty: No tak i ta prosta, która przecina najwyżej wskazuje na wierzchołek, którego trzeba użyć do obliczenia największej wartości i jest to punkt (1,4), więc największa wartość wychodzi −1... Sama się chyba już w tym pogubiłam. Jeżeli ktoś by miał wystarczająco dużo czasu i cierpliwości, proszę o wytłumaczenie