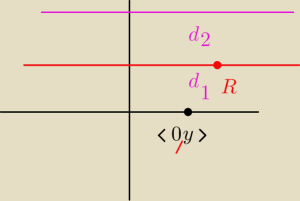
 Na osi OX wyznacz punkt równanie odległe od prostych x + y − 6 = 0 i 7x − y =0
d1 = d2
więc
obliczam odległość miedzy tymi prostymi
R(0,6)
0+y=6
7x−y=0
A=7
B= −1
C=0
d1 = | 7*0 + (−1)*6 + 0 |/ √ 72 + 12 = 6/pP50} :C
Na osi OX wyznacz punkt równanie odległe od prostych x + y − 6 = 0 i 7x − y =0
d1 = d2
więc
obliczam odległość miedzy tymi prostymi
R(0,6)
0+y=6
7x−y=0
A=7
B= −1
C=0
d1 = | 7*0 + (−1)*6 + 0 |/ √ 72 + 12 = 6/pP50} :C
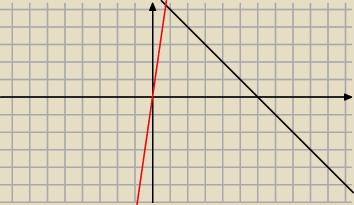 To sa wykresy rownan tych prostych
To sa wykresy rownan tych prostych
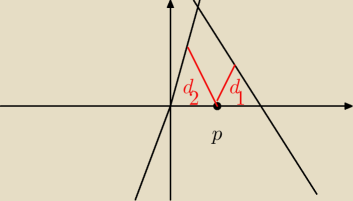 Ale to nie zmienia faktu , że
d1 = d2
hmm i tak nie wiem jak to miałabym zrobić
Ale to nie zmienia faktu , że
d1 = d2
hmm i tak nie wiem jak to miałabym zrobić
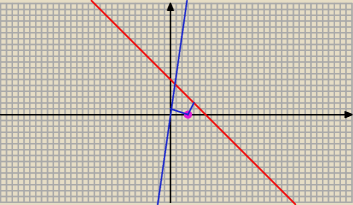 x + y − 6 = 0
7 x − y = 0
P − leży na osi OX , więc P = ( xo ; 0 )
x + y − 6 = 0
7 x − y = 0
P − leży na osi OX , więc P = ( xo ; 0 )
| I 1 xo + 1*0 − 6 I | I xo − 6 I | |||
d1 = | = | |||
| √ 12 + 12 | √2 |
| I 7 xo − 1*0 + 0 I | I 7 xo I | |||
d2 = | = | |||
| √72 + (−1)2 | √50 |
| I xo − 6 I | I xo I | I 7 xo I | |||
= | = | ||||
| √2 | √ 2*25 | 5 √2 |