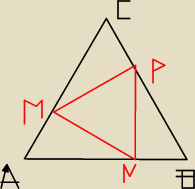
optymalizacja MX: Hmmm skomplikowane Proszę o pomoc, podpowiedź, wskazówkę Pomocy:( Trójkąt równoboczny ABC ma bok długości 10cm. Na jego bokach obrano punkty M, N, P tak, że |AM|=|BN|=|CP| (jak na rysunku) Jak należy wybrać punkty M N i P aby pole trójkąta MNP było najmniejsze?

MX: prosze o pomoc

Mateusz:

	c2*√3
Zauważ, że trójkąt w MNP też jest równoboczny, jego pole jest równe
	4

Mamy warunki |AM|= |BN| = |Cp|=x oraz |Ap| = |CN| = |BM| = 10−x korzystamy z twierdzenia cosinusów

	π
c2 = x2 +(10−x)2 −2x(10−x)cos		dalej juz sobie chyba poradzisz
	3

Mozna tez 2 sposobem obliczamy pole trójkąta ABC które jest równe 25√3 to pole trójkąta MNP

	3x(10−x)√3		3x(x−10)√3
jest równe 25√3−		= 25√3+		teraz szukamy najmniejszej
	4		4

wartości tej funkcji

MX: szukamy ja poprzez wyznaczenie x tak dzieki za pomoc

MX: yyy cos mi nie wyszło