trygonometria
Saizou : Pomożecie, mam nadzieję że tak

| | π | |
Udowodnij że sinx<x dla x∊(0: |
| ) |
| | 2 | |
nie mam pojęcia jak to ruszyć, jakieś wskazówki ?
12 paź 16:53
Kacper:
Saizou nie umiesz?

12 paź 16:55
Saizou :
Karcper po to chyba poszedłem na studia żeby się nauczyć

12 paź 16:57
Saizou : *Kacper
12 paź 16:57
Kacper: Mam problem z rysunkiem

12 paź 17:02
miki:
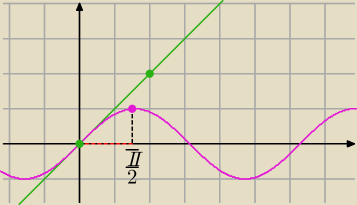
12 paź 17:05
Kacper:
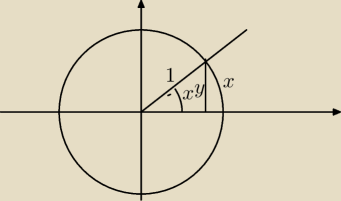
| | l | |
Z definicji miary łukowej kąta x= |
| ⇒x=l |
| | r | |
Prawdziwa jest nierówność y<x
| | π | |
Zatem sinx<x dla x∊(0, |
| ) |
| | 2 | |
12 paź 17:05
Saizou : jakie to było banalne

12 paź 17:09
Saizou : to chyba przez to ze jestem chory że nie widzę takich prostych zależności
12 paź 17:10
Saizou : a jeszcze jedno jak udowodnić wzór sin(x+y)=sinxcosy+cosxsiny dla dowolnych x,y
12 paź 17:19
12 paź 17:20
ICSP: Poszukać się nie chce ?

12 paź 17:21
Saizou :
ICSP dzięki za link

12 paź 17:21
PW:
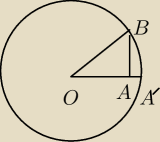
Normalnie rysujesz okrąg o promieniu 1 i w nim trójkąt prostokątny OAB o wierzchołku kąta x w
środku okręgu O. Dowcip polega na tym, że
miara kąta to długość łuku, a więc
sinx = |AB| < |A'B| < |łuku A'B| =
x.
A' to punkt wspólny prostej OA z okręgiem.
12 paź 17:23
PW: Znowu nie zdążyłem

12 paź 17:24









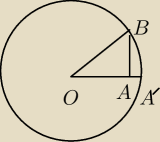 Normalnie rysujesz okrąg o promieniu 1 i w nim trójkąt prostokątny OAB o wierzchołku kąta x w
środku okręgu O. Dowcip polega na tym, że miara kąta to długość łuku, a więc
sinx = |AB| < |A'B| < |łuku A'B| = x.
A' to punkt wspólny prostej OA z okręgiem.
Normalnie rysujesz okrąg o promieniu 1 i w nim trójkąt prostokątny OAB o wierzchołku kąta x w
środku okręgu O. Dowcip polega na tym, że miara kąta to długość łuku, a więc
sinx = |AB| < |A'B| < |łuku A'B| = x.
A' to punkt wspólny prostej OA z okręgiem.
