prawdopodobienstwo andzia: Z kwadratu jednostkowego wybrano punkt (x,y). Wyliczyć prawdopodobieństwo, że ℙ(|x−y|)<¹₄) Bardzo proszę o rozwiązanie

Hurwitz: A jaki rozkład prawdopodobieństwa zadano na tym kwadracie? Jeżeli jednostajny to wystarczy obliczyć pole tego kawałka kwadratu, który spełnia warunek |x−y|<1/4. O ile kwadrat jednostkowy to dla Ciebie [0,1]x[0,1].

andzia: myślę ze chodzi własnie o to, ale jezeli moglabym prosic o pełniejsze rozwiazanie bo zupelnie nie wiem jak to zrobic dalej

Hurwitz: Prawdopodobieństwo zdarzenia A={(x,y)∊[0,1]x[0,1]: |x−y|)<1/4} to całka po zbiorze A z gęstości rozkładu. Z zadania wynika, że gęstość to f(x,y)=1 na kwadracie; po za nim zero. Więc ∫_A f(x,y)dxdy= ∫_A 1 dxdy = Pole (A)= 7/16.

Mila:

	1
(|x−y|)<		⇔
	4

	1		1
y>x−		i y<x+
	4		4

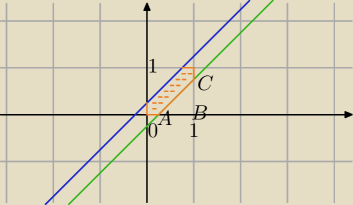
Wybierasz punkt z obszaru zacieniowanego

	1
P(|x−y|<		)=1−2*PΔABC
	4

	1		1		1
x−		=0⇔x=		⇔A(		,0)
	4		4		4

	1		3		3
1−		=		⇔C=(1,		)
	4		4		4

	3
|AB|=
	4

	3
|BC|=
	4

	1		1		3		3		9		7
P(|x−y|<		)=1−2*PΔABC=1−2*		*		*		=1−		=
	4		2		4		4		16		16

Całkę masz u kolegi 16:30.