Kule styczne w sześcianie mietek3: Witajcie. Czy istnieje taka sytuacja, że w sześcianie są dwie kule: jedna styczna do wszystkich ścian sześcianu i druga styczna do trzech ścian sześcianu i styczna zewnętrznie do poprzedniej kuli?

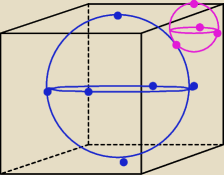
Kejt: hmm.. nie wiem, czy widać wystarczająco dobrze... te kropki to punkty styczności.

PW: Piękny rysunek, Kejt. Górną czerwoną kropkę przeniósłbym jednak na przekątną górnej ściany (nie krytykuję, bo sam nie umiem rysować). Pytanie "czy istnieje" wymaga oczywiście rachunków. Czy jest prawdą, że punkty styczności kul ze ścianami sześcianu należą do płaszczyzn wyznaczonych przez przekątne przeciwległych ścian?

Kejt: Wiem, PW ręcznie wyszłoby mi to znacznie lepiej... przy tego rodzaju rysunkach ograniczenie wstawiania kropek, ogólnie rysowania w obrębie wyświetlanych kratek to duża przeszkoda. Przynajmniej dla mnie.

PW: A masz jakąś koncepcję wyliczenia? Myślałem o przekrojach, dlatego o tych przekątnych ścian napisałem.

Kejt: Koncepcję mam, ale nie wiem czy dobrą. Skończę pisać projekt i narysuję to dokładniej, w jakimś programie. Dam znać wieczorem, czy się udało.

PW: Może niepotrzebnie się zastanawiamy. Wystarczyłoby chyba stwierdzić, że dla dowolnej r > 0 istnieje kula o promieniu r styczna do trzech ścian wzajemnie prostopadłych (wyznaczonych przez trzy wzajemnie prostopadłe półproste o wspólnym początku). Mówiąc potocznie − każdą kulkę da się upchać w rogu pokoju (jeśli się w tym pokoju zmieściła). Nasza kulka musi mieć odpowiedni promień, tak by zetknęła się z dużą kulą.