Zilustruj na płaszczyźnie zespolonej roevs: Zilustruj na płaszczyźnie zespolonej: {z c C: arg(i/z)<=3pi/4}

Kacper: Co to jest argument liczby zespolonej?

roevs: Wartość kąta α, jaki tworzy wektor wodzący liczby z dodatnią półosią Re z. Można też definiować jako wartość kąta, która spełnia układ równań cosα i sinα. Wyszło mi, że cos tego kąta powinien przyjmować wartości z przedziału <−√2/2; 1>

roevs: Ale po prostu nie wiem, może mam zaćmienie, może to coś innego − nie potrafię w ogóle tego zaznaczyć.

Kacper: Pokaż rachunki. Masz odpowiedź do tego?

roevs: Nie mam odpowiedzi. A moje rachunki sprowadzają się tylko do tego, że 0<=α<=3pi/4, z czego wynika, że cos może przyjmować takie, a nie inne wartości.

Kacper: Jaki cosinus?

roevs: cosα może przyjmować wartości: <−√2/2; 1> a cosα to nic innego jak stosunek części rzeczywistej do modułu

Kacper:

	i		3π
To w takim razie zaznacz na płaszczyźnie zespolonej {z∊C: arg(		)=		}
	z		4

Hurwitz: Pamiętaj, że arg (i/z) = arg (i) − arg (z) +2kπ. Stąd, uwzględniając, że arg(i) = π/2, wyliczasz arg (z) i masz warunek. PS> W treści zadania powinno być też jakieś ograniczenie od dołu, np. 0<arg(i/z)<=3π/4. W przeciwnym przypadku otrzymasz całą płaszczyznę; chyba, że arg to argument główny liczby zespolonej.

roevs: Tak, arg to argument główny. Dlaczego arg(i) ma wartość π/2?

roevs: Okej, już wiem. Głupie pytanie W takim razie mam: 0 ≤ arg(i/z) ≤ 3π/4; 0 ≤ arg(i) − arg(z) ≤ 3π/4; −π/2 ≤ −arg(z) ≤ 3π/4; Więc: −π/2 ≤ −arg(z) i −arg(z) ≤ 3π/4; arg(z) ≥ π/2 i arg(z) ≥ 3π/4; Czyli mam po prostu zaznaczyć przedział od π/2 do 2π?

roevs: Przepraszam, błąd. Powinno być finalnie: arg(z) ≤ π/2 i arg(z) ≥ −3π/4 Mniejsze od π/2 rozumiem, ale większe od −3π/4? Mam od 360 stopni odjąć 135, i wtedy wynikiem będzie zakres od 225 stopni do 90 (zgodnie z ruchem wskazówek zegara)?

Hurwitz: Skoro 0 ≤ arg(i) − arg(z) ≤ 3π/4 to −π/2≤−arg(z)≤3π/4−π/2=π/4 Czyli ostatecznie −π/4≤arg(z)≤π/2 O 2kπ możesz zapomnieć bo wszystko mieści się w okresie.

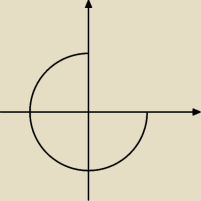
roevs: Chodzi mi stricte jak to zaznaczyć na płaszczyźnie zespolonej. arg(z)≥π/2 to rysunek wyżej. A co z −π/4≤arg(z)?

roevs: Nie wiem dlaczego zaznaczyłem arg(z)≥π/2 jak powinienem zaznaczyć arg(z)≤π/2. Znów błąd. No w każdym razie wtedy zaznaczenie jest odwrócone − od 0 do π/2.

PW:

	i		i z̅
zz̅ = |z|2, a więc		=		, a ponieważ mianownik jest dodatnią liczbą
	z		|z|2

rzeczywistą, wynika stąd, że

	i		π
Arg		= Arg(iz̅) = Argi + Argz̅ = Argz̅ +		.
	z		2

Mamy zatem zaznaczyć takie liczby z, że z̅ spełnia nierówność

	π		3π
Argz̅ +		<
	2		4

	π
Argz̅ <
	4

Rysujemy najpierw te z̅ , a potem odpowiednie z.

roevs: Dlaczego nie uwzględniamy mianownika?

PW: Podzielenie (pomnożenie) liczby zespolonej przez dodatnią liczbę rzeczywistą nie zmienia jej argumentu. Jeżeli liczbę zespoloną wyobrazić sobie jako koniec kijka o początku w (0,0), a jej argument główny jako kąt nachylenia tego kijka do osi rzeczywistej, to jest oczywiste, że zmiana długości kijka nie zmieni jego kąta nachylenia.

roevs: Dziękuję! Już wszystko jasne Pozdrawiam