zepsolone
Paulina:
|z+1|+z−=3
jak rozbić moduł ?
√(x+1)2+y2 ?
10 paź 19:22
Mila:
z=x+iy
|x+iy+1|+x−iy=3
|(x+1)+iy|+x−iy=3
√(x+1)2+y2+x−iy=3
10 paź 19:33
Paulina:
Czyli dobrze myślałam, dziękuję.
10 paź 19:36
Mila: 
10 paź 19:42
Paulina:
Mila masz jeszcze dużo czasu ? W wtorek mam wejściówkę na ćwiczeniach z liczb zespolonych, z
indukcji i logiki

A nie za bardzo wszystko rozumiem.
10 paź 19:47
Paulina:
Coś mi nie wyszło
 √(x+1)2+y2
√(x+1)2+y2+x−yi=3
x
2+2x+1+y
2=3−x x≤3 y=0
x
2+2x+1+y
2=x
2−6x+9
8x=8
x=1
z=1 w odpowiedzi jest x=2
Więc co jest źle ?
10 paź 19:57
Mila: x,y∊R
Część urojona : y=0
√(x+1)2+x=3
|x+1|+x=3
x≥−1
x+1+x=3
2x=2
x=1
z=1+0i=1
=========
|x+1|=−x−1 dla x<−1
−x−1+x=3
−1=3 sprzeczność , brak rozwiązań.
Sprawdź czy dobrze przepisałaś treść zadania.
10 paź 20:19
razor: gdzie zgubiłaś −yi?
10 paź 20:19
PW: Zbyt nerwowo patrzysz na problem
z̅ = 3 − |z+1|.
Prawa strona jest liczbą rzeczywistą, a to oznacza, że również z̅ jest rzeczywista, i w
konsekwencji z jest też rzeczywista. Rozwiązujemy równanie
x = 3 − |x+1|, x∊R
i po ptokach. Rozwiązaniem jest oczywiście liczba 1.
10 paź 20:19
Kacper: 5 razy pisałem to samo co PW i non stop kasuje mi

10 paź 20:20
Paulina:
Dziękuję, zapomniałam o oczywistości ze wzorem skróconego mnożenia..
10 paź 20:24
PW: Kto do licha kasuje? Jest tu jakiś szkodnik?
10 paź 20:25
Mila:
?
10 paź 20:27
Paulina:
Znajdź Arg(1−i) ?
10 paź 20:49
PW: Rozpatrywana liczba to
(1, −1))
− w takiej sytuacji najlepiej ją zaznaczyć w układzie współrzędnych i popatrzeć "trzeźwem
okiem" − co to jest argument?
10 paź 20:53
Paulina:
a nie liczyć cosφ i sinφ ?
10 paź 20:55
PW: Nie pytali o to, odpowiedzieć na pytanie − jaki jest argument tej liczby (i jeżeli to widzimy w
sposób oczywisty, to nie liczymy). To mają być prościutkie zadania pod tytułem "rozumie − nie
rozumie", jak sama piszesz "wejściówka".
10 paź 21:01
Mila:
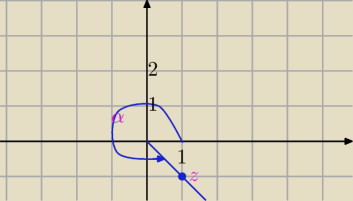
z=1−i to punkt płaszczyzny (1,−1)
10 paź 21:06
Paulina:
Nie wiem, inaczej nie potrafię
10 paź 21:06
Mila:
Argument nie może przekraczać 2π. Popatrz na definicję.
10 paź 21:08
10 paź 21:16
Mila:
Tak.
10 paź 21:23
Paulina:
A to można robić graficznie ? (szybciej) Nie zdążyłam zanotować wszystkiego

10 paź 21:24
Mila:
Jeśli się da to tak. Łatwe przyklady.
4+0i
2+2i
0+2i
−3+0i
0−i
10 paź 21:28
Paulina:
Dobrze postaram się porobić takie przykłady i dojdę może do wprawy

Jednak matematyka w lo to nie to samo co studia

10 paź 21:35
10 paź 21:41
PW: Liczby z0 = 1, z1, z2, z3, z4 oraz z5 na płaszczyźnie zespolonej stanowią wierzchołki
sześciokąta foremnego wpisanego w okrąg o promieniu 1. Podaj ich postać trygonometryczną (ale
nic nie licz, po prostu podaj).
10 paź 21:42
Paulina:
Bez liczenie nie bardzo jeszcze wiem...
10 paź 21:45
PW: To jest właśnie pytanie o argument − jest interpretacja geometryczna, trzeba z niej od czytać
moduły i argumenty i zapisać liczby w postaci trygonometrycznej.
10 paź 21:54
Mila:
Jak to nie wiesz, narysuj w układzie wsp. sześciokąt i będzie wszystko jasne, to bardzo ładne
zadanie i pożyteczne.
10 paź 21:55
Paulina:
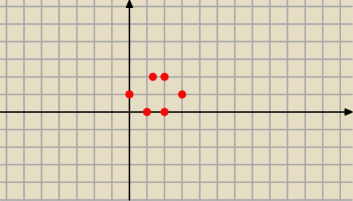
?
10 paź 21:58
PW: Przepraszam, nie napisałem, że okrąg ma środek (0,0), a Ty oczywiście utrudniłaś sobie

10 paź 22:06
Paulina:
Trzeba założenie ?
z
−≠1
z+1=−z
−+1
10 paź 22:38
Paulina: ?
10 paź 22:50
Mila:
Rozwiąż i potem pomyślisz , czy potrzeba.
10 paź 22:58
Paulina:
x+yi+1=−(x−yi)+1
x+yi=−x+yi+1
10 paź 23:08
Mila:
Chyba jesteś zmęczona.
ź≠1
z=−ź
z+ź=0
x+iy+x−iy=0 niezależnie od wyboru y∊R wyrazy (iy) i (−iy) zredukują się do zera.
2x=0⇔x=0
z=0+iy,y∊R
======
10 paź 23:15
Paulina:
Idę spać od 7 rano siedzę nad matematyką, próbując zrozumieć wykłady.
Dziękuję i dobranoc.
10 paź 23:17
Mila:
Dobranoc. Spokojnie. Wszystko będzie dobrze.

10 paź 23:19
Paulina:
z=0 a właśnie yi się uprościło więc nie ma części Im z

11 paź 18:43
Mila:
Im (z) jest tak jak napisałam 23:15
x=0 i y∊R
Jeśli rozwiązujesz równanie:
a) 2x=0 to x=0 jedno rozw.
b) 2x+1=2x+3
1=3 sprzeczność, brak rozwiązań
c) A równanie :
2x+4=2x+4 jest spełnione dla każdej liczby
x∊R − nieskończenie wiele rozwiązań
i właśnie z częścią Im masz taką sytuację.
Spr. weźmy np:
z=5i
| | 5i+1 | | 5i+1 | |
L= |
| = |
| =−1 |
| | −5x−1 | | −(5i+1) | |
11 paź 18:58
Paulina:
Dziękuję serdecznie, Mila jesteś kochana

11 paź 22:39
Lidka:

11 paź 22:40
Paulina:
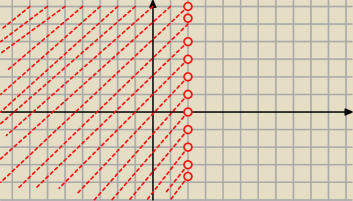
Narysuj na płaszczyźnie zespolonej
{z: rez<2}
ok ?
12 paź 17:52
Lidka:
Dobrze, załóż nowy wątek.
12 paź 17:54

 A nie za bardzo wszystko rozumiem.
A nie za bardzo wszystko rozumiem.
 √(x+1)2+y2+x−yi=3
x2+2x+1+y2=3−x x≤3 y=0
x2+2x+1+y2=x2−6x+9
8x=8
x=1
z=1 w odpowiedzi jest x=2
Więc co jest źle ?
√(x+1)2+y2+x−yi=3
x2+2x+1+y2=3−x x≤3 y=0
x2+2x+1+y2=x2−6x+9
8x=8
x=1
z=1 w odpowiedzi jest x=2
Więc co jest źle ?

 z=1−i to punkt płaszczyzny (1,−1)
z=1−i to punkt płaszczyzny (1,−1)

 Jednak matematyka w lo to nie to samo co studia
Jednak matematyka w lo to nie to samo co studia
 ?
?





 Narysuj na płaszczyźnie zespolonej
{z: rez<2}
ok ?
Narysuj na płaszczyźnie zespolonej
{z: rez<2}
ok ?