działanie Janusz :

2x+1
	−1=?
x+2

NaPotęgeMatematyki: O czymś nie wiem czy tego nie da się policzyć?

Janusz : nie da sie do wspolnego mianownika?

Kacper: a polecenie jakieś jest?

Janusz : to jest wyjęte z zadania z szeregiem miałem założenie że q<1

	2x+1
a q to
	x+2

więc rozpatruję na przypadki że q<1 i q>−1 no i ta dziedzina troche dziwna wyszła xd

Janusz : wartość bezwzględna z q*

Janusz :

Janusz : nie wierze żeby nikt nie potrafił ;>

Kacper: Napisz konkretnie, że chcesz rozwiązań układ nierówności

	2x+1
−1<		<1
	x+2

A ty to tak piszesz, że nikt cię nie rozumie.

Janusz : no więc jak rozwiązać taki układ?

Kacper: Najpierw

	2x+1
−1<
	x+2

potem

2x+1
	<1
x+2

i na koniec część wspólna obu rozwiązań.

Janusz : no przecież tak robiłem... i mi nie wyszło patrz

2x+1
	−1<0
x+2

2x
	<0 mnoze razy mianownik2
x+2

(2x)(x+2)=0 x=0 lub x=−2 cos mi tu nie pasuje...

o nie: jeśli a)

	2x+1
q<1 =>		−1<0
	x+2

2x+1 − x+2
	<0
x+2

x−1
	<0
x+2

b)

	2x+1
q>−1 =>		+1>0
	x+2

2x+1 + x+2
	>0
x+2

3x+3
	>0
x+2

z dziedziny tylko −2 się wyklucza obliczasz i część wspólna

Janusz :

	x+2
czyli ta 1 cała to jest		?
	x+2

ale ja jestem głupi

Janusz :

	2x+1		1
ja sprowadzałem do wspólnego mianownika i wyszło		−
	x+2		x+2

Bogdan:

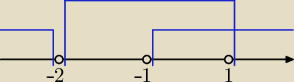
	2x + 1		2x + 1		2x + 1 + x + 2
(1)		> −1 ⇒		+ 1 > 0 ⇒		> 0
	x + 2		x + 2		x + 2

3(x + 1)(x + 2) > 0 ⇒ x∊(−∞, −2)∪(−1, +∞) i

	2x + 1		2x + 1		2x + 1 − x − 2
(2)		< 1 ⇒		− 1 < 0 ⇒		< 0
	x + 2		x + 2		x + 2

(x − 1)(x + 2) < 0 ⇒ x∊(−2, 1) (1)∩(2): x∊(−1, 1)

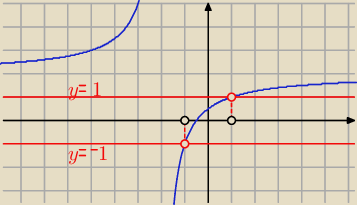
Bogdan: interpretacja graficzna tej podwójnej nierówności

pigor: ..., lub np. tak : −1< ^2x+1_x+2<1 i (*) x≠−2 ⇔ |^2x+1_x+2|<1 /* |x+2| ⇒ ⇒ |2x+1| < |x+2| ⇔ (2x+1)² < (x+2)² ⇔ 4x²+4x+1−x²−4x−4 < 0 ⇔ ⇔ 3x²< 3 ⇔ |x|< 1 ⇔ −1< x< 1, stąd i z (*) ⇔ x∊(−1;1) ...