prawdopodobienstwo cntrl: Z urny, w której jest tyle samo kul czarnych, białych i zielonych, wyjęto bez oglądania jedną kulę, a następnie wylosowano dwie kule. Prawdopodobieństwo tego, że są one białe wynosi

	1
		. Ile kul było w urnie na początku?
	11

Kacper: Proponuje drzewo stochastyczne.

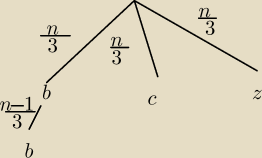
cntrl: coś takiego? i

n2 − n		1
	=
9		11

cntrl:

	n−2
a i jeszcze *
	3

cntrl: Nie wiem jak uwzględnić, że wylosowano kulę białą

PW:

	n
Zwyczajowo przy gałązkach piszemy prawdopodobieństwa, skąd więc		?
	3

Myślę, że nie rozumiesz na czym polega drzewko (to tak jak ja).

cntrl:

	n
no własnie... dlaczego napisałem
	3

nie mam pojęcia o co mi chodziło

Mila: Losowanie pierwsze C lub B lub Z n− liczba kul każdego koloru

	n		1
P(C1)=		=
	3n		3

	1
P(B1)=
	3

	1
P(C1)=
	3

Gdy wylosowano jedna kulę, to w urnie zostało (3n−1) kul (n−1)C, nB,nZ lub nC,(n−1)B, n Z lub nC,nB,(n−1)Z

1

n

n−1

1

n−1

n−2

P(BB)=

*

*

+

*

*

+

3

3n−1

3n−2

3

3n−1

3n−2

	1		n		n−1
+		*		*		=
	3		3n−1		3n−2

	1		3n2−5n+2
=		*		z treści zadania:
	3		9n2−9n+2

1		3n2−5n+2		1
	*		=
3		9n2−9n+2		11

rozwiąż.

cntrl: Wychodzi mi 3 ... W odpowiedziach jest 12, chyba jestem już zmęczony

cntrl: znaczy wychodzi mi 4

Kacper: To licz ponownie

Kacper: Ale to przecież jest dobrze

cntrl: 4 jest dobrze? xd

Kacper: Zobacz co oznacza twoje policzone n, a o co pytali w zadaniu.

cntrl: Dzięki

Mila: n=4, czyli 3*4=12