Stereometria Stachu: A może takie zadanie. Krawędź podstawy i wysokość ściany bocznej poprowadzona z wierzchołka ostrosłupa prawidłowego czworokątnego mają długości 2 alfa. Oblicz cosinus kąta dwuściennego miedzy sąsiednimi ścianami bocznymi. Sporządź rysunek pomocniczy i zaznacz na nim wymieniony w zadaniu kąt dwuścienny.

AROB: pomogę, poczekaj.

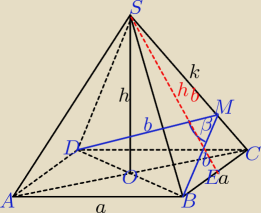
AROB: Najpierw poślę rysunek bryły.

Bogdan: Dobranoc

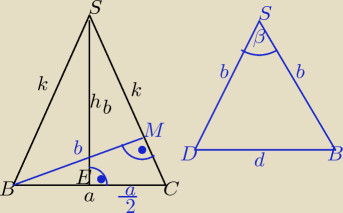
AROB: Dane: a = 2α, h_b =2α cosβ = ? Z ΔECS obliczamy długość krawędzi bocznej k:

	a
hb2 + (		)2 = k2
	2

k² = (2α)² + α² k² = 5α² ⇒ k = α√5 ΔSEC ∼ ΔBCM

	b		hb
Stąd:		=
	a		k

	b		2α		4α
		=		⇒ b =
	2α		α√5		√5

Znając b wchodzimy do ΔDBS, w którym zastosuję wzór cosinusów. Jeszcze bok d: jest to przekątna podstawy (kwadratu), zatem d = a√2 = 2α√2 Ze wzoru cosinusów mamy: d² = b² + b² − 2*b*b*cosβ (2α√2)² = 2b² − 2b²cosβ

	4α		4α
8α2 = 2* (		)2 − 2* (		)2 * cosβ
	√5		√5

	16		16
8α2 = 2 *		α2 − 2 *		α2cosβ
	5		5

	32		32
8α2 =		α2 −		α2cosβ
	5		5

	32		32		32
		α2cosβ =		α2 − 8α2 /:		α2
	5		5		5

	5		5		1
cosβ = 1 − 8 *		= 1 −		= −
	32		4		4

AROB: Dobranoc Eto i Bogdanie.

Stachu: Dzieki

AROB:

Magda: witam serdecznie odświeżam kotlet

Magda: zadanie rozumiem jak najbardziej ale nurtuje mnie pewna rzecz... dlaczego nie można tego konta ustawić aby był w połowie krawędzi C ? legenda:

	c
1−
	2

	c
2−
	2

Magda: **kąta przepraszam za błędy ort... reasumując zauważyłam że ta płaszczyzna jest ustawiona celowo pod kątem prostym do krawędzi bocznej.. a interesuje mnie to czy można ustawić aby była w połowie krawędzi bocznej.. czy ktoś mógłby mi to doradzić

Magda:

	|CS|
1−
	2

	|CS|
2−
	2

Magda: .