monotonicznosc
Kris: Zbadaj monotonicznosc ciagu
bn = n2 − 10n + 10
bn+1 = (n+1)2 − 10(n+1) + 10 = n2 − 8n + 1
bn+1 − bn = 2n − 9
Funkcja jest zatem rosnąca ?
9 paź 22:37
Bogdan:
Nie. Ciąg nie jest monotoniczny
9 paź 22:40
Bogdan:
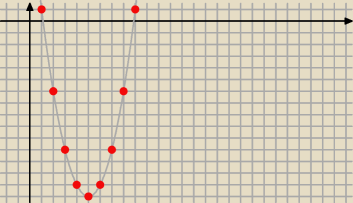
9 paź 22:44
Kris: Ok dzięki
9 paź 22:44
Kris: Bogdan a to nie jest tak ze n ∊ N ? I to ze wzrostem n rosnie ?
9 paź 23:05
Kris: aa widze juz na wykresie bez sensu pytanie
9 paź 23:05
Kris: an = n2 − n + 2
an+1 = (n+1)2 −(n+1) + 2 = n2 + n + 2
an+1 − an = 2n
w tym wypadku takze bedzie nie monotoniczny bo wystepuje n ?
9 paź 23:32
Janek191:
a n + 1 − an = 2n > 0 dla dowolnego n ∊ ℕ1 , więc ciąg ( an) jest rosnący.
10 paź 07:12
