funkcje wielu zmiennych c--: podaj opis wędrówki po : 1. łamanej { (x, y) :y=|x| ∧ x∈[−2,2] } 2. łamanej { (x, y) :y=| |x−1|−2 | ∧ x∈[−5,5] } 3. brzegu kwadratu o wierzchołkach: (−1,−1),(1,−1),(1,1),(−1,1) 4. brzegu jakiegoś trójkąta 5. po ósemce

Godzio: Chodzi o parametryzacje?

c--: mój pomysł na pierwsze to : x(t)=2t y(t)=2|t| gdzie t∊[−1,1] mamy wtedy x∊[−2,2] y∊[0,2] i zależność y=|x|

c--: tak

Godzio: Jak dla mnie ok.

c--: na drugie też prosto x(t)=t t∊[−5,5] y(t)= | |t−1|−2| i wszystko się zgadza [ w 1. i 2. moim przykładzie każdy odcinek pokonywany jest raz, ale można i po tym samym odcinku ruszać się kilkukrotnie ]

c--: problem pojawia się przy 3. proszę o wskazówki jak do tego się zabrać

c--: muszę przejść na 3 zmienne ?

c--: muszę przejść na 3 zmienne ?

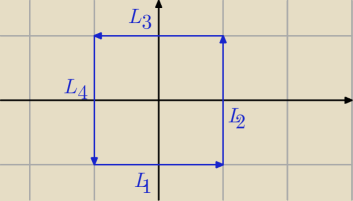
Godzio: L₁: x(t) = t, y(t) = −1, t ∊ [−1,1] L₂: x(t) = 1, y(t) = t, t ∊ [−1,1] L₃: x(t) = 1 − t, y(t) = 1, t ∊ [0,2] L₄: x(t) = −1, y(t) = 1 − t, t ∊ [0,2]

c--: super dzięki zaraz sam spróbuję z tym Δ

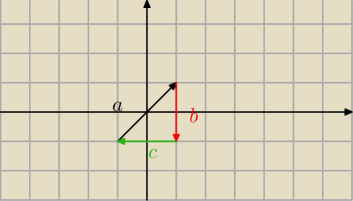
c--: a: x(t) = t, y(t) = t, t ∊ [−1,1] b: x(t)=1 y(t)=1−t t∊[0,2] c: x(t) = 1−t, y(t) = −1, t ∊ [0,2]

Godzio: No i git

c--: teraz jeszcze ósemka i gotowe zaraz się z nią zgłoszę

Godzio: I jak, idzie coś?

c--: mam pomysł tylko jeszcze realizuję

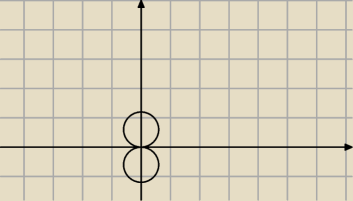
c--: x(t)=3sin(t) to nam da r=3 t ∊[0,2π] y(t)=3cos(t)+3 x(t)=3sin(t) to nam da r=3 t ∊[0,2π] y(t)=3cos(t)−3

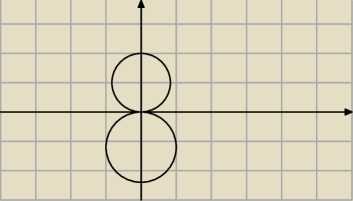
c--: taka najbanalniejsza ósemka, myślałem jeszcze nad takimi x(t)=3sin(t) to nam da r=3 t ∊[0,2π] y(t)=3cos(t)+3 x(t)=4sin(t) to nam da r=3 t ∊[0,2π] y(t)=4cos(t)−4

c--: tutaj miało być r1=3 r2=4

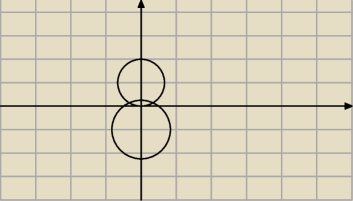
c--: i nad taką ale jej równania nie potrafiłbym napisać tak aby pozbyć się części z dolnego okręgu wchodzącej w górny , musiałbym pewnie znaleźć najpierw punkty przecięcia, a potem pozbyć się tego jakoś możesz to sprawdzić [ 1. i 2. ósemkę]

Godzio: Gdybyś podał środki to mógłbym się ustosunkować, ale pewnie jest ok − o to chodziło

c--: 1.ósemka górna część : środek (0,3) dolna część środek (0,−3) 2. ósemka górna część : środek (0,3) dolna część środek (0,−4)

Godzio: jeszcze mnie zastanawia jedno (niestety to miałem daaaawno temu i mało pamiętam) czy parametryzacja musi być "po kolei" tzn. czy nie trzeba parametryzować każdego łuku z osobna i iść tak jak po ósemce: lewa górna −> prawa dolna −> lewa dolna −> prawa górna? Nie mam pojęcia, ale może Ty wiesz

c--: tak tak, faktycznie tak powinno być, bo to ma być odzwierciedleniem ruchu, czyli pomysł dobry tylko teraz muszę zmienić nieco dane by ruch się zgadzał

c--: x(t)=3sin(t) to nam da r=3 t ∊[0,2π] y(t)=3cos(t)+3 najpierw górny okrąg

	π		5π
x(t)=4sin(t) to nam da r=4 t ∊[		,		]
	2		2

y(t)=4cos(t)−4 tutaj zaczynamy od samej góry punktu stycznego z osią x i lecimy po okręgu aż zajdziemy ponownie do (0,0) jeśli zakres t zwiększe o kolejne krotności 2π będą to kolejne ruchy po tej ósemce

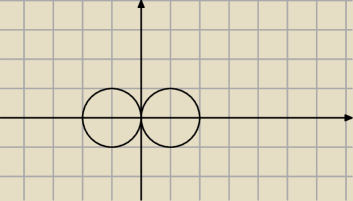
c--: x(t)=5sin(t)−5 t∊[0,2π] y(t)=5cos(t) x(t)=5sin(t)+5 t∊[π,3π] y(t)=5cos(t) środki (−5,0) (5,0) r=5 ruch od lewego od (0,0) przeciwnie do zegara do (0,0) i teraz zgodnie z zegarem prawy okrąg od (0,0) do (0,0)

[C[czerwony]]c--: tam przy kwadracie aby się zgadzalo : x=t t∊[−1,1] y=−1 x=1 y=t −2 t∊[1,3] x=4−t t∊[3,5] y=1 x=−1 y=6−t t∊[5,7]