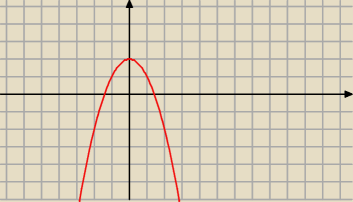
roznowartosciowosc funkcji 5-latek: Dobry wieczor Takie polecenie mam : Zbadaj czy funkcja y=−x²+2 jest roznowartosciowa Otoz D_f=R i z definicji roznowartosciowosci mam ze x₁≠x₂ to x₁−x₂≠0 i f(x₁)≠f(x₂) to f(x₁)−f(x₂)≠0 To zapisuje sobie ze f(x₁)=−x₁²+2 i f(x₂)= −x₂²+2 To licze f(x₁)−f(x₂)= −x₁²+2−(−x₂²+2)= −x₁²+x₂²=−(x₁²−x₂²)= −(x₁−x₂)(x₁+x₂) TO wobec tego wychodzi mi ze x₁−x₂≠0 i x₁+x₂tez≠0 bo x₁≠x₂ wyszlo mi ze f(x₁)−f(x₂)≠0 i ta funkcja jest roznowartosciowa (co jest nieprawda Wobec tego gdzis muszse robic blad w obliczeniach Prosze wobec tego o wskazanie tego bledu

5-latek: Polecenie jest dokladnie takie samo jak napisalem .

razor: załóżmy że f(x₁) = f(x₂) → x₁ = x₂ −x₁²+2 = −x₂²+2 x₁² = x₂² x₁ = x₂ lub x₁ = −x₂ z prawdy wynika fałsz, więc nasze założenie jest sprzeczne → funkcja nie jest różnowartościowa

5-latek: Dobrze. To czyli z definicji nie obliczysz tylko dowod nie wprost Moze tak byc gdyz to zadanie jest z rozszerzenia dziekuje

Godzio: Fachowe pokazanie, że funkcja NIE JEST różnowartościowa polega na wskazaniu KONTRPRZYKŁADU, czyli pokazujemy, że dla x₁ = 1 ≠ −1 = x₂ mamy f(1) = 1 = f(−1), zatem funkcja nie jest różnowartościowa. W przeciwnym wypadku przeprowadzamy dowód z definicji

5-latek: Witaj Godzio Dziekuje za odpowiedz Tobie rowniez Robilem to zadanie z definicji gdyz jest to zadanie z 1 klasy liceum i to przed funkcjami kwadratowymi (ksiazka z 2009r Przyjalem ze ten 1 klasista nie zna z gimnazjum wykresu funkcji kwadratowej . No chyba ze jest inaczej i zna to wtedy pokazujemy kontrprzyklad tak jak napisales jeszce raz dziekuje

Godzio: Nie trzeba znać funkcji kwadratowej, jedynie co trzeba wiedzieć to to, że x² ma taką samą wartość dla x = k jak i dla x = −k, a to wie każdy gimnazjalista, który umie potęgować

5-latek: Dobrze