Styczna do okręgu James: Wyznacz równanie stycznej do okręgu (x+1)²+(y−2)²=9 równoległej do prostej x+2y+3=0

===: współczynnik znasz przyrównaj styczna ... jeden punkt ... Δ=0 (otrzymasz dwie wartości b)

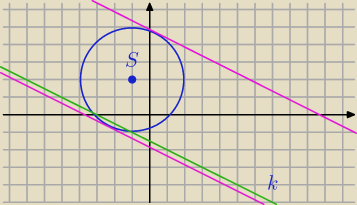
Mila: k: x+2y+3=0

	−1		3
y=		x−
	2		2

Styczna jest równoległa do prostej k, to jest postaci: s: x+2y+D=0 Aby wyznaczyć wsp. D możemy skorzystać z własności , że odległość punktu S od stycznej jest równa promieniowi okręgu r=3. S=(−1,2)

	| −1+2*2+D|		|3+D|
d=3=		⇔3=
	√12+22		√5

|3+D|=3√5⇔ 3+D=3√5 lub 3+D=−3√5 D=3√5−3 lub D=−3√5−3 Mamy dwie styczne: s₁: x+2y+3√5−3=0 s₂: x+2y−3√5−3=0 =================

James: Dzięki

Mila: