Zadanie z parametrem Magda: dla jakich wartości parametru m równanie x² − 3x + m − 3 = 0 ma dwa pierwiastki rzeczywiste takie, że suma ich odwrotności jest równa 3 ?

razor:

	1		1		x1+x2
Δ > 0 i		+		= 3 →		= 3
	x1		x2		x1*x2

Podstaw i licz

Magda: Założyłam, że delta > 0 i 1/x1 + 1/x2 = 3 Z delty wyszło mi że −4m + 21> 0, więc 21/4 > m czyli m ∊ (−∞, 21/4). Co do pierwastków ze wzorów Viete'a wychodzi że (x1+x2)/x2x1 czyli po podstawieniu 3/m−3 = 3. Gdzie popełniłam błąd ?

Mat: Nie powinno być delta większa bądź równa 0?

Magda: właśnie nie wiem...

razor: mnie uczyli że dwa pierwiastki − Δ > 0 ale w różnych szkołach różnie podchodzą do tego problemu

Mat: Ponieważ równanie ma dwa pierwiastki rzeczywiste i nigdzie nie ma napisane że są różne. Jak dla mnie Δ ≥ 0

Magda: dzięki. Tylko nadal nie wiem gdzie zrobiłam źle... Czy mogłby ktoś to rozwiązać ? prosze

razor:

	3
jest dobrze, po prostu rozwiąż teraz to równanie		= 3
	m−3

Magda: wyszło mi m=4 dobrze ?

razor: a na maturze ktoś ci powie czy jest dobrze? podstaw m = 4 do równania i sprawdź czy suma odwrotności pierwiastków jest równa 3

Magda: Bo nie wiem jak to sprawdzić. Podstawić 4 pod m do równania kwadratowego? No i w poleceniu było wyznacz wartości, nie jedną i nie wiem czy dobrze...

===: 3/(m−3)=3 ⇒ 3=3m−9 ⇒ m=4 ... i co tu źle?

Magda: po podwstawieniu wychodzi 1=0 co oczywiscie jest nieprawda

Mat: −b/a a nie b/a

Mat: Wychodzi dobrze tylko ja mam teraz pytanie czy pisać że 4 nalezy do tej dziedziny mniejszych od 21/4 czy to nie jest dziedziną? I w odpowiedzi już tylko że dla m=4?

Magda: tak zrobiłam : −b/a / c/a = −b/c ⇒ 3/ m−3 = 3 ⇒ 3m−9 = 3 ⇒ 3m = 12 ⇒ m=4

razor: pisze się tak

	x1+x2
Δ > 0 i		= 3
	x1*x2

	21
(m <		i m = 4) → m = 4
	4

Magda: ale jak jest dobrze ? po podstawieniu m do równania kwadratowego wychodzi, że 1=0, więc albo źle sprawdzam albo jest źle zrobione

Mat: Oblicz odwrotność tych pierwiastków jeszcze raz ale zamiast c (m−3) podstaw 4−3 czyli

Mat: I wtedy dokonujesz sprawdzenia

Magda: No to wtedy dobrze wychodzi... ale to co, mam zignorować, że w podstawianiu do rownania kwadratowego jest źle?

razor: x²−3x+m−3 = 0 podstawiam m = 4 x²−3x+4−3 = 0 x²−3x+1 = 0 Δ = 9 − 4 = 5, √Δ = 5

	3−√5		3+√5
x1 =		, x2 =
	2		2

1		1		2		2		2(3+√5)+2(3−√5)
	+		=		+		=		=
x1		x2		3−√5		3+√5		(3−√5)(3+√5)

	6+2√5+6−2√5		12		12
		=		=		= 3
	32−√52		9−5		4

Magda: Aaaaah rozumiem ! czyli się podstawia tylko m do równania kwadratowego. Ja jeszcze przyjełam dowolny x ze np. x=2, x=3. I potem do odwrotności pierwiastków. Dzieki wielkie!

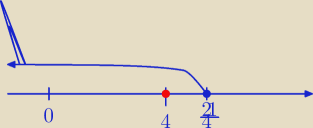
daras: obojętnie czy jest Δ ≥ 0 czy > 0, to koniunkcją tych dwu zbiorów jest m = 4

Magda: nie umiem robić sprawdzeń :') jeszcze raz dziekuje wszystkim za pomoc