wierzchołki trapezu bla bla: wyznacz wierzchołki trapezu równoramiennego ABCD, AB>CD, AB||CD mając rownanie jego symetrii y=−¹₂x+2 i wiedząc, że jej punkty przecięcia z osiami układu współrzędnych są środkami podstaw, punkt A(1,−6), a jedna podstawa jest dwa razy krótsza od drugiej

Eta: Już jestem , pomagam Rysuję.

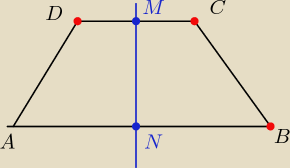Eta: Nie rysuję tego trapezu w układzie współrzędnych ( sam sobie narysujesz i sprawdzisz ) Widzę bla bla , że sumiennie zgłebiasz wiedzę , więc podam w skrócie rozwiązania z pewnością sobie poradzisz więc tak: prosta MN : y = −¹₂x +2 jest osią sym trapezu , więc przecina podstawy w punktach N i M , które są jednoczesnie środkami podstaw: AB i CD punkt N; to punkt przecięcia prostej y = −¹₂x+2 z osią OX " " M " " " " " z osią OY N: y =0 −¹₂x +2 = 0 => N ( 4,0) M: x =0 y = +2 => M( 0,2)

	xA+ xB		yA+yB
A(1, −6) więc: xN=		.... yB=
	2		2

to; x_B= 2*x_N −x_A i y_B= 2*y_N − y_A x_B = 7 i y_B = 6 ( policz, tak wyjdzie) B(7,6)

	xC+xD		yC+yD
podobnie: xM=		... yM=
	2		2

to: x_C+x_D=0 i y_C +y_D = 4 x_D= − x_C i y_D = 4 − y_C → → → → ponieważ IABI = 2IDCI i AB II DC to współrzędne wektorów równoległych są równe: AB= [6,12] 2DC= [2(x_C−x_D), 2(y_C−y_D)] porównując współrzędne otrzymasz: x_C−x_D = 3 i y_C− y_D= 6 x_D= −x_C i y_D= 4 − y_C rozwiazując układy równań otrzymasz D i C odp: D( −³₂, −1) C( ³₂, 5) Dobranoc

Eta: Oczywiście .....uwzględniając waruneki zadania ,że AB > DC i trapez równoramienny.

bla bla: Eta jesteś wielka spędziłam nad tym zadaniem mnóstwo czasu i nic nie wymysliłam Dziekuje bardzo