Dwa moduły
ToTamir: Mam takie zadanie ( jak i kilkanaście podobnych ): |x−1|+|x+2|=3
Nie jestem w stanie tego ogarnąć. Bardzo proszę o wytłumaczenie mi tego na tym jednym
przykładzie.
8 paź 19:57
Mila:
 |x−1|+|x+2|=3
|x−1|+|x+2|=3
Jeśli chodzi o rozwiązanie równania to tak:
1) |x−1|=x−1 ⇔x−1≥0⇔x≥1
|x−1=−x+1 dla x<1
2) |x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
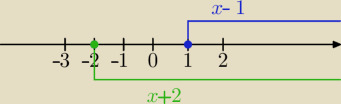
Zaznaczę to na osi liczbowej:
Teraz rozważamy równanie w przedziałach:
a) x<−2
−x+1−x−2=3⇔−2x=4⇔x=−2 ∉D
b) x∊<−2,1)
−x+1+x+2=3⇔3=3⇔każda liczba z przedziału <−2,1) spełnia równanie
c)x≥1
x−1+x+2=3
2x+1=3
2x=2
x=1∊<1,
∞)
Odp x∊<−2,1> (nieskończenie wiele rozwiązań.)
========================================
W następnym wątku narysuję wykres funkcji
f(x)=|x−1|+|x+2|
9 paź 00:01
Mila:
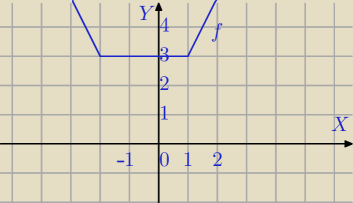
f(x)=|x−1|+|x+2|
9 paź 00:04
pigor: ..., zauważ, że ten przykład
|x+3|+|x−1|=3 (i
jemu podobne)
jest akurat najłatwiejszy z interpretacji odległości na osi OX, bo na niej
odległość miejsc zerowych pod modułami |1−(−2)| = |−2−1|= |3|=3 − prawej
stronie danego równania, dlatego rozwiązaniem jest przedział <−2;1>. ...

9 paź 00:25
 |x−1|+|x+2|=3
Jeśli chodzi o rozwiązanie równania to tak:
1) |x−1|=x−1 ⇔x−1≥0⇔x≥1
|x−1=−x+1 dla x<1
2) |x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
Zaznaczę to na osi liczbowej:
Teraz rozważamy równanie w przedziałach:
a) x<−2
−x+1−x−2=3⇔−2x=4⇔x=−2 ∉D
b) x∊<−2,1)
−x+1+x+2=3⇔3=3⇔każda liczba z przedziału <−2,1) spełnia równanie
c)x≥1
x−1+x+2=3
2x+1=3
2x=2
x=1∊<1,∞)
Odp x∊<−2,1> (nieskończenie wiele rozwiązań.)
========================================
W następnym wątku narysuję wykres funkcji
f(x)=|x−1|+|x+2|
|x−1|+|x+2|=3
Jeśli chodzi o rozwiązanie równania to tak:
1) |x−1|=x−1 ⇔x−1≥0⇔x≥1
|x−1=−x+1 dla x<1
2) |x+2|=x+2 dla x≥−2
|x+2|=−x−2 dla x<−2
Zaznaczę to na osi liczbowej:
Teraz rozważamy równanie w przedziałach:
a) x<−2
−x+1−x−2=3⇔−2x=4⇔x=−2 ∉D
b) x∊<−2,1)
−x+1+x+2=3⇔3=3⇔każda liczba z przedziału <−2,1) spełnia równanie
c)x≥1
x−1+x+2=3
2x+1=3
2x=2
x=1∊<1,∞)
Odp x∊<−2,1> (nieskończenie wiele rozwiązań.)
========================================
W następnym wątku narysuję wykres funkcji
f(x)=|x−1|+|x+2|
 f(x)=|x−1|+|x+2|
f(x)=|x−1|+|x+2|
