Miary kątów w trójkącie,środkowa,wysokość,dwusieczna MonicaAlexandra: W ΔABC z wierzchołka kąta C poprowadzono wysokość,dwusieczną i środkową,które podzieliły kąt na 4 równe części. Oblicz miary kątów ΔABC. Nie mam kompletnie pomysłu na to zadanie Ciągle mi się oznaczenia z miarami kątów upraszczają i nic konkretnego nie mogę znaleźć żeby to rozwiązać ;c

Kacper: A masz odpowiedź?

MonicaAlexandra: Niestety nie mam gdybym miała to może by się udało jakoś od końca dojść do tego i potem analizować jak inaczej to zrobić a tak to nie mam pojęcia

Kacper: Jakoś nie wydaje mi się, żeby taki trójkąt istniał, ale mogę się mylić

MonicaAlexandra: Ja już sama nie wiem... Możliwe,że osoba,która dała mi to zadanie pominęła coś w treści...

Andrzej: Policzyłem

===: ... a dlaczego nie ?

Andrzej: To trójkąt o kątach 90, 22.5, 67.5 Policzyłem z twierdzenia o dwusiecznej. Mam wrażenie, że to trochę długa metoda i da się szybciej. Ale udało się

MonicaAlexandra: Tak na idiotę dopasowywując sobie miary kątów niby wychodzi,że może być np 80,70,30... ale czy to ma sens?

MonicaAlexandra: A mogłabym poprosić o bardziej szczegółowe rozwiązanie?

MonicaAlexandra: I który kąt jest który oraz ile wynosi ta 1/4 tego kąta który został podzielony?

Kacper: Ma ktoś krótki sposób na to zadanko? Andrzej rzeczywiście da się policzyć, ale pisania sporo

MonicaAlexandra: A mógłbyś wprowadzić na rysunku oznaczenia lub coś w ten deseń? Bo nie wiem jak oznaczyć boki itp żeby mi jakieś sensowne działania wyszły ;c

Andrzej w pracy: Tu Andrzej, tylko że teraz z pracy piszę. Rozłączyło mi net wczoraj. A znalazłem banalny sposób na to zadanko − w dwóch linijkach niemal. Ludziki, to prościutkie, na poziomie 5. klasy jest Na samych kątach się liczy − suma kątów w trójkącie. Jak nie wymyślicie do wieczorka, to napiszę. Idę uczyć dzieci, pozdrawiam.

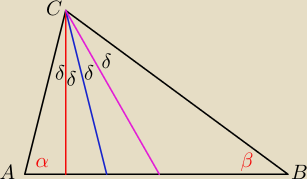
Janek191: γ = 4 δ

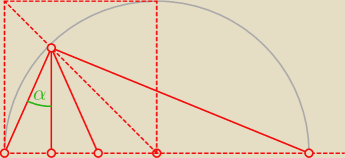
===: ... i wszystko jasne− (dla Ciebie pozostaje wykazanie, że ten trójkąt musi być prostokątny

PW: Samymi kątami wyliczyć się nie da. Musi być uwzględniony choćby warunek podziału podstawy na dwa równe odcinki przez środkową. Niech środkowa ma długość d, podstawa 2a, a pozostałe boki trójkąta b i c. Z twierdzenia sinusów wynikają równości:

	a		d
(1)		=		,
	sin(3α)		sin(90° − α)

a w drugim z trójkątów

	a		d
(2)		=		.
	sinα		sin(90°− 3α)

Wyliczenie, że kąty w odpowiednich trójkątach są równe (90°−α) oraz (90°−3α) jest łatwe. Z równości (1) i (2) po podzieleniu stronami i zastosowaniu wzoru redukcyjnego wynika

	sinα		cos(3α)
		=
	sin(3α)		cosα

sinαcosα = sin(3α)cos(3α) 2sinαcosα = 2sin(3α)cos(3α) sin(2α) = sin(6α), dla kątów ostrych takich że 4α < 180° równanie to ma jedno rozwiązanie 6α = 180°−2α 8α = 180° α = 22°30''. Andrzej wczoraj oświadczył, że zastosował twierdzenie o dwusiecznej, więc przedstawiam inny sposób, ale nie wierzę w cudowny sposób "dla dzieci".

Kacper: Ja też chętnie zobaczę "cudowny" sposób tylko z kątów. PW nieźle. W sumie to prostsze niż korzystanie z twierdzenia o dwusiecznej.