nierówność z dwoma zmiennymi sei: jak rozwiązać (x²+y²)>0

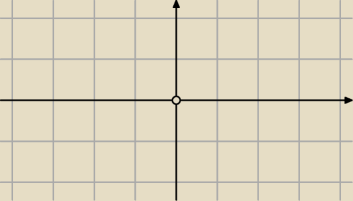
Bogdan: x² + y² > 0 ⇒ x, y ∊ R \{0} Każdy punkt płaszczyzny oprócz punktu O=(0, 0)

Bogdan: a przy okazji: x² + y² = r² to równanie okręgu o środku O=(0, 0) i promieniu r

sei: dziękuję bardzo. pierwotnie też miałam takie rozwiązanie, że to punkt (0,0). ale tak się zagalopowałam w filozofowaniu (przykład to fragment z założenia dziedziny funkcji wielu zmiennych), że nie wierzyłam, że odpowiedź może być tak prosta dziękuję!

sei: a czy gdybym miała takie coś: x²−y²>0 to mogę zrobić to analogicznie, przyjmując założenie, że to również równanie okręgu x²+(−1)y²=r² S=(0,−1) r=0 ?

razor: x²−y² to nie jest równanie okręgu

sei: przepraszam, pomyliło mi się we wzorze mnożenie z odejmowaniem. jak zatem rozwiązać przykład x²−y²>0?

razor: (x−y)(x+y) > 0 kiedy iloczyn dwóch liczb jest dodatni?

sei: kiedy obie są dodatnie lub kiedy obie są ujemne