geometria tyka: Środkowe trójkąta poprowadzone do boków o długości 16 i 12 są prostopadłe. Oblicz długość trzeciego boku.

tyka: ponawiam

tyka: czy ktoś mógłby mi pomóc ?

Mila: Liczę. Cierpliwości.

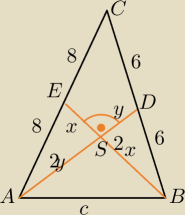
Mila: EB⊥AD środkowe dzielą się w stosunku 2:1 licząc od wierzchołka ΔDSB,ΔESA,ASB są prostokątne. x²+(2y)²=8² y²+(2x)²=6² x²+4y²=64 4x²+y²=36 stąd y²=36−4x² Podstawiamy do pierwszego x²+4(36−4x²)=64

	80		16
stąd x2=		=
	15		3

	16
x2=
	3

=====

16
	+4y2=64 /:4
3

4
	+y2=16
3

	44
y2=
	3

============ W ΔABS: (2y)²+(2x)²=c² 4y²+4x²=c²

	44		16
c2=4*		+4*
	3		3

	44		16
c2=4*(		+		)
	3		3

c²=4*20 c²=80 c=√80 c=4√5 ============

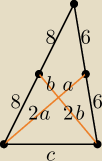Bogdan: albo a² + 4b² = 36 4a² + b² = 64 + −−−−−−−−−−−−

	4
5a2 + 5b2 = 100 /*		⇒ 4a2 + 4b2 = 80 = c2 ⇒ c = √80 = 4√5
	5

Mila: Sprawność obliczeniowa i jasność umysłu niech żyje.

Bogdan:

Eta: x²+4y²=64 ⇒ 4y²=64−x²

	320
4x2+y2=36 /*4 ⇒ 16x2+4y2=144 ⇒ 16x2+64−x2=144 ⇒ 15x2=80 ⇒4x2=
	15

	20		880
to: 4y2=64−		⇒ 4y2=
	80		15

	880+320
c2=4x2+4y2 ⇒ c2=		= 80 ⇒ c=√80= 4√5
	15

Eta:

Eta: I to jest przewaga ...... męskiego mózgu nad móżdżkiem kobiety

tyka: Dziekuje wszystkim