nierówności
Adrian: wyznacz dziedzinę oraz zbiór rozwiązań nierówności
√3+xx ≤0
−x√x+2≥0

do klasówki pyka a ja mam wątpliwości co do tych przykładów. Wiem że dziedzina to zbiór
liczb spełniających dane równanie, ale do tych przykładów mam wątpliwości i ciągle coś knoce

7 paź 19:35
Adrian: pierwiastek z 3+x przez x jest mniejszy równy zero
minus x przez pierwiastek z x+2 jest większy równy zero
7 paź 19:36
5-latek: czemu nie moze rownac sie mianownik ?
czemu jest rowne wyrazenie pod pierwiastkiem?
7 paź 19:39
Adrian: mianownik nie moze równać się zeru
wyrażenie pod pierwiastkiem jest liczbą Rzeczywistą dodatnią
7 paź 19:47
5-latek: Wyrazenie pod pierwiastkiem jest liczba nieujemna czyli tez z definicji pierwiastka
algebraicznego moze rownanc sie 0 weic jest ≥0
Przyklad a) dziedzina x ≠0 i 3+x≥0 i wyznacz ja
7 paź 19:52
Adrian: chyba muszę zmienić nick bo jest 3 różnych Adrianów..
7 paź 19:52
Adrian: a) D: x ≠0 ∧ 3+x≥0⇔D:x ≠0 ∧x≥−3⇔D: <−3,+∞)−{0} ?
7 paź 19:57
Adrian: czyli w b będzie:
D: −x≥0 ∧√x+2 ≥ 0 ⋁ (−x≤0 ∧√x+2 ≤ 0 −niemożliwe⇒D: −x≥0 ∧√x+2 ≥ 0 ⇔ −x≥0 ∧x∊<−2,+
∞)⇔D: x≤0
∧x∊<−2,+
∞)⇔D:<−2,0>

coś sknociłem...
7 paź 20:02
Metis:
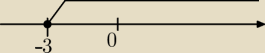
Ustalając dziedzinę parzysz zawsze na mianownik − nie można dzielić przez 0... oraz liczbe
podpierwiastkową, która musi być większa, równa 0.
Wiec :
x+3≥0
x≥−3 oraz x≠0
Rysujemy przedział na osi, prościej.
Teraz musimy usunąc 0 z naszego przedziału. Zatem:
Dziędziną bedzie suma przedziałów:
x∊<−3,0)U(0,+
∞)
Od razu widać że 0 nie należy do przedziału.
7 paź 20:10
Adrian: podpunkt a) <−3,+
∞)−{0} napisałem, a co sknociłem w b)

7 paź 20:16
Metis: W b) zajmujesz się tylko mianownikiem.
Uważając na to że tym razem liczba podpierwiastkowa musi być tylko większa od 0.
Dlaczego ?
7 paź 20:17
Adrian: liczba jest większa od zero gdy licznik i mianownik są albo dodatnie albo ujemne jednocześnie.
tam mam √x+2 w mianowniku, a mianownik nie może być równy 0 więc √x+2≠0. Liczba
podpierwiastkowa musi być zawsze nieujemna więc √x+2≤0 czyli D:<−2,+∞)−{0} ?
7 paź 20:23
Metis: Poczekaj na kogoś doświadczonego. Nie chce wprowadzać w błąd.
7 paź 20:31
Adrian: oki będę zaglądał co pare minutek, dziękuje

7 paź 20:33
undefined: Po prostu pierwiastek stopnia parzystego nie może być z liczby ujemnej, więc x≥0 i w mianowniku
nie może występować 0, więc x≥0 ∧ x≠0 daje nam x>0.
7 paź 20:39
5-latek: W drugim wyrazeniu to co jest pod pierwiastkiem musi byc >0 a nie ≥0
Dlaczego ? bo jesli bedzie rowne 0 to dostaniesz niedowolone dzielenie przez 0
TO wyrazenie pod pierwiatkiem masz w mianowniku a dzielic przez 0 nie wolno
czyli x+2>0 to x>−2 czyli x nalezy (−2,oo)
7 paź 20:39
7 paź 20:40
Metis: Czyli pisałem dobrze

7 paź 20:41
Adrian: więc w b) będzie:
−x/√x+2≥0 ∧D: (−2,+oo)⇔−x≥0⇔x≤0⇔x∊(−2,0)
a)
√3+x/x≤0 ∧D:<−3,+oo)−{0}⇔√3+x≤0⇔x=−3
dobrze to jest zrobione ?
7 paź 20:53
Metis: do a) masz post 20:10
do b)
D: x+2> 0
x>−2
x∞(−2,+∞)
7 paź 20:56
Metis: x∊(−2,+∞)
7 paź 20:58
Adrian: zbiór rozwiązań nierówności
czy dobrze wyznaczylem te zbiory, ja juz sie ucze tyle godzin ze nic nie rozumiem z tego
do b)
D: x+2> 0
x>−2
x∞(−2,+∞)
7 paź 21:02
Metis: O co teraz pytasz?
7 paź 21:06
Adrian: jakie będzie rozwiązanie tych nierówności
7 paź 21:11
Adrian: nie dziedzina tylko rozwiązanie
7 paź 21:12
Metis: Co proponujesz?
7 paź 21:46
Adrian: a) √3+x/x≤0 ∧D:<−3,+oo)−{0}⇔√3+x≤0⇔ x=−3
b)−x/√x+2≥0 ∧D: (−2,+oo)⇔−x≥0⇔x≤0⇔ x∊(−2,0)
7 paź 21:50
Metis: Jak z nierówności nagle może Ci wyjść równość

Zastanów się dobrze! Pomyśl dla jakich x nierówność zostanie spełniona.
7 paź 21:52
Adrian: o Boże serio już mam wyłączony mózg... chwila pomyślę..
7 paź 21:58
Adrian: a)√3+x/x≤0 ∧D:<−3,+oo)−{0}⇔√3+x≤0⇔równanie sprzeczne ?
b)jw.
7 paź 22:04
";();: Ty serio jesteś taki głupi....Nie wiem co tutaj robisz i w dodatku o 22:04.
9 paź 16:04
 do klasówki pyka a ja mam wątpliwości co do tych przykładów. Wiem że dziedzina to zbiór
liczb spełniających dane równanie, ale do tych przykładów mam wątpliwości i ciągle coś knoce
do klasówki pyka a ja mam wątpliwości co do tych przykładów. Wiem że dziedzina to zbiór
liczb spełniających dane równanie, ale do tych przykładów mam wątpliwości i ciągle coś knoce

 coś sknociłem...
coś sknociłem...
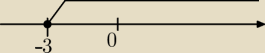 Ustalając dziedzinę parzysz zawsze na mianownik − nie można dzielić przez 0... oraz liczbe
podpierwiastkową, która musi być większa, równa 0.
Wiec :
x+3≥0
x≥−3 oraz x≠0
Rysujemy przedział na osi, prościej.
Teraz musimy usunąc 0 z naszego przedziału. Zatem:
Dziędziną bedzie suma przedziałów:
x∊<−3,0)U(0,+∞)
Od razu widać że 0 nie należy do przedziału.
Ustalając dziedzinę parzysz zawsze na mianownik − nie można dzielić przez 0... oraz liczbe
podpierwiastkową, która musi być większa, równa 0.
Wiec :
x+3≥0
x≥−3 oraz x≠0
Rysujemy przedział na osi, prościej.
Teraz musimy usunąc 0 z naszego przedziału. Zatem:
Dziędziną bedzie suma przedziałów:
x∊<−3,0)U(0,+∞)
Od razu widać że 0 nie należy do przedziału.



 Zastanów się dobrze! Pomyśl dla jakich x nierówność zostanie spełniona.
Zastanów się dobrze! Pomyśl dla jakich x nierówność zostanie spełniona.