wykres z wartością bezwględną zuz.: chodzi o narysowanie funkcji f(x)= |y|≥|x+1| z |x+1| nie ma problemu, tylko zastanawiam się jak zinterpretować |y|. czy cała ta funkcja nie będzie wyglądać po prosu jak |x+1| skoro wszystkie |y| będą dodatnie?

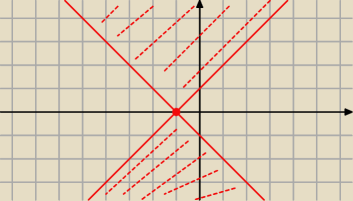
MQ: obszary zakreślone wraz z brzegiem, bo ≥

rp88: |y|≥|x+1| potraktujmy to jako dwa warunki

⎧	y≥0
⎨		lub
⎩	y≥|x+1|

⎧	y<0
⎨		lub
⎩	−y≥|x+1|

dalej już łatwo

pigor: ..., w czym problem |y| ≥ |x+1| ⇔ |y| ≥ |x+1| i |x+1≥0 ∀x∊R ⇒ ⇒ { (x,y)∊R² ; y ≤−|x+1| v y ≥ |x+1| }, a ten zbiór masz właśnie narysowany powyżej przez MQ. ...

pigor: ..., a poprawnie to chodziło ci o : narysuj zbiór (obszar) F={ (x,y): |y|≤ |x+1| } , a nie żądną funkcję f(x) −−−−−−−−−−−−−−−−−−−−−−− a jesli już, to ten zbiór może być np.dziedziną (obszarem określoności) jakiejś funkcji dwóch zmiennych z= fx,y). ...