Funkcja liniowa Monika: Funkcja f: R→R jest malejącą funkcją liniową taką, że

	1
f(−		) = 0.
	3

	3
Jeśli g(x) = f(−		− 2x), to jakie jest miejsce zerowe funkcji g?
	2

5-latek: Witaj Moniko Sam chcialbym poznac rozwiazanie tego zadania , poniewaz takie idiotyczne zadania nie byly wymyslane wtedy kiedy ja sie uczylem .

Monika: Właaaaśnie nigdzie nie mogę znaleźć podobnego

5-latek: Ktos to napewno rozwiaze ale co moge zauwazyc to miejscem zerowym funkcji f:R→R jest punkt

	1
(0 −		)
	3

Monika: a może:

	3		1
−		− 2x −= −		?
	2		3

Monika:

	7
taak, w odpowiedziach jest −
	12

5-latek: Nie wiem . Tylko po co podali ze ta funkcja f:R→R jest malejaca ?

Monika: dla zmyły

5-latek: Wydaje mi sie ze tak bedzie .

Monika: a coś takiego: Do zbioru X należą punkty leżące na prostej y = 34x+400 których współrzędne (x,y) spełniają następujące warunki: x i y są liczbami całkowitymi oraz x<0 ∧ y>0. Wyznacz liczbę elementów zbioru X.

	1600
doszłam do x > −		∧ x < 0
	3

Monika:

	3
* y =		x + 400
	4

J:

	−1		1		1
f(x) = ax + b , f(		) = 0 ... 0 = a(−		) + b ⇔ b =		a
	3		3		3

	1
.. f(x) =ax +		a
	3

	3		1
g(x) = a(−		− 2x) +		a ..... i teraz :
	2		3

	3		1		−7
0 = a(−		− 2x) +		a ⇔ x =		.... szukane miejsce zerowqe
	2		3		12

5-latek: Ja mysle sobie tak wyliczylismy ze x>−533,33333 Wiec dla x=−533 do x=−1 i x musi byc calkowite y jest >0 i teraz musimy sprawdzic dla ktorych x_ow y jest calkowite Ale nie wiem czy dobrze mysle

J: .....cześć 5−latek.. .... łapiesz 1 zadanie ?

5-latek: Dzieki J za pierwsze A to drugie ? . Bo tez bede teraz powtarzal wlasnosci funkcji i funkcje liniowa

5-latek: Tak J pierwsze przemysle (tylko wroce od lekarza ) Teraz tez zauwazylem swoj blad . Bo punkt zerowy to nie (0,−1/3 ) tylko (−1/3,0) post 10:56

J:

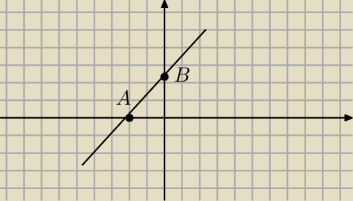
	400
...popatrz na rysunek... A(−		, 0 )
	34

	400
skoro x < 0 i y > 0 (obie całkowite) .. to:		< x < 0 ...
	34

i wybrać liczby całkowite z tego przedziału..

5-latek: Bardzo dziekuje CI Mysle tez ze Monika wysle caluski za popowiedzi Teraz juz muszese jechac . Po poludniu jak bedziesz to napiszse czy wszystko rozmiem

Monika:

	400
ale skąd to −		? Powinno wyjść 133 takich liczb
	34

J: ... to miejsce zerowe tej funkcji: y = 34x + 400. masz teraz: x = −11 , −10 , −9 , .... −1 i dla każdego z nich wybierasz y całkowite takie,że: y < 0 < f(x) ..... i te wszystkie punkty (x,y) należą do zbioru X

Monika:

	3
ale ta funkcja to y =		x + 400
	4

to pokombinuję analogicznie

Monika: ale w tym wypadku wychodzi za dużo, żeby liczyć na piechotę każde y

J: .. dziewczyno ... to pisz poprawnie... napisałaś: y = 34x + 400 ... nikt tu nie jest jasnowidzem !

Monika: Napisałam potem poprawioną wersję

J:

	1600
....postępuj analogicznie , jak napisałem , tylko zmieni się miejsce zerowe ...
	3

TakeItEasy: y = ³₄ − 400 Xmin = ⁻¹⁶⁰⁰₃ dla y = 0 Xmin ~= 533.(3) y = ³₄ * 533 + 400 = 0,25, wiec nie należy do całkowitych y = ³₄ * 532 + 400 = 1, wiec spełnia warunki zad. i idąc dalej(ciąg arytmetyczny): An = 543 A1 = 4 r = 4 An = A1 + (n − 1)r n = ^{An − A1}_r + 1 n = 133. Tyle mamy par Dobrze to? Pozdrawiam, TakeItEasy =)

Boniek: Z tym zadaniem można sobie bardzo łatwo poradzić wystarczy sobie wyobrazić co ile współrzędnych x i y będziemy mieli całkowite współrzędne y to co 3 x co 4. Ale mamy podany punkt przecięcia z osią y czyli 400, dzięki podzieleniu odległości na odległości co 3 tzn podzieleniu 400 na 3 otrzymamy 133 z kawałkiem. Czyli odp 133