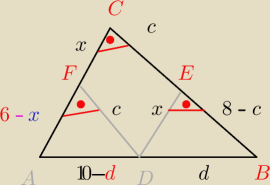
Twierdzenie Talesa Code::Blak: Z punktu D należące do AB trójkąta prostokątnego ABC poprowadzono odcinki DE i DF w sposób pokazany na rysunku. Przyprostokątne tego trójkąta mają długości |AC|=6 i |BC|=8. Wyznacz długość odcinka AD taką , aby ole prostokąta CEDF Moje obliczenia: AB= 10 AC= 6 BC= 8 ... dalej mi wychodzą bezsensowne proporcje pomóżcie

Eta: ..... "aby pole prostokąta ..... co? dokończ treść zadania

Code::Blak: aby pole prostokąta było największe bardzo przepraszam chochlik się wdał

Code::Blak: Macie ?

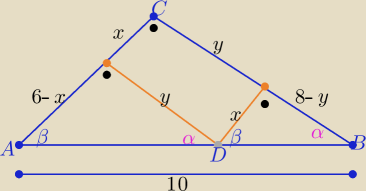
Eta: Z podobieństwa trójkątów ABC i ADF i DBE z cechy (kkk)

|DE|		|EB|		x		8−y
	=		⇒		=		⇒ ........... 4y=24−3y
|AC|		|CB|		6		8

P(DEFC)= x*y ⇒ 4P=4x*y = (24−3y)*y= −3y²+24y −−− funkcja osiąga maksimum

	−24		24−3y
dla ymax=		= 4 to xmax =		= ...=3
	−6		4

|AD|		y
	=		⇒ |AD|=........
|AB|		|BC|

Eta: Żyjesz?

Code::Blak: tak dzięki

Eta:

Code::Blak: mam sobie sam obliczyć ?

Eta: Jasne ..... dokończyć .......to już mały pikuś

Code::Blak: Jak ja bym chciał mieć z tobą stały kontakt to nawet nie wiesz Dziękuje

5-latek: Ty Code Black nie podlizuj sie tak do mojej Pani z przedzszkola

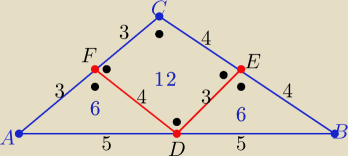
Eta: To teraz zauważ,że największe pole ma prostokąt , gdy punkty D E F są środkami odpowiednich boków AB BC AC P(DEFC)=12

Eta: Dla "małolatka"

Code::Blak: Mam jeszcze jedną prośbę o zrobienie tego zadania poniżej Na jednym z boków trójkąta ABC obrano punkt P i poprowadzono przez nieco proste równoległe do pozostałych boków. Podzieliły one trójkąt na dwa trójkąty o polach S1 i S2 i równoległobok. Wyznacz pole trójkąta ABC w zależności od S1 i S2.

5-latek: Dobry wieczor . Pozdrawiam

5-latek: Przepraszam ale zapomnialem podziekowac za piekny rysunek