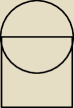
 Okno ma kształt prostokąta zakończonego na górze półkolem (jak na rysunku) obwód okna ma 4m.
Oznacz długości podstawy prostokąta przez x, Następnie:
a) Napisz wzór funkcji pola P powierzchni okna w zależności od x
b) określ dziedzinę funkcji P
c) wyznacz długość podstawy prostokąta tak, aby pole powierzchni okna było największe.
Uzasadnij
Okno ma kształt prostokąta zakończonego na górze półkolem (jak na rysunku) obwód okna ma 4m.
Oznacz długości podstawy prostokąta przez x, Następnie:
a) Napisz wzór funkcji pola P powierzchni okna w zależności od x
b) określ dziedzinę funkcji P
c) wyznacz długość podstawy prostokąta tak, aby pole powierzchni okna było największe.
Uzasadnij

| x | 1 | x | ||||
promień pólkola r = | , obwód okna: 2h + x + | 2π( | ) = 4 | |||
| 2 | 2 | 2 |
| 1 | x | |||
P(x) = x*h + | π( | )2 ... oblicz h z pierwszego równania i podstaw.... | ||
| 2 | 2 |