Geometria Marcin: Próbowałem zrobić te 3 zadania, ale niestety nie umiem... 1. Dany jest trójkąt równoboczny ABC. Punkt P leży wewnątrz tego trójkąta. Niech X, Y, Z będą rzutami prostokątnymi punktu P odpowiednio na proste BC, CA, AB. Wykaż że suma PX+PY+PZ jest wartością stałą i nie zależy od wyboru punktu P. 2. Dany jest romb o polu=960 i wysokości 48. Oblicz obwód tego romba i sumę jego przekątnych. 3. Dany jest romb ABCD. Odcinek AB = 10, kąt ABC ma miarę 45 stopni. Oblicz długości jego p[przekątnych i pole tego rombu.

Marcin: Ponawiam

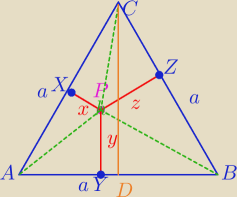
Mila: CD= h− Wysokość ΔABC

	1
PΔABC=		a*h
	2

PY⊥AB, PZ⊥BC, PX⊥AC , to odcinki x, y, z są wysokościami w trójkątach: ΔABP,ΔBCP, ΔACP

	1		1		1
PΔABC=		*a*y+		*a*z+		*a*x⇔
	2		2		2

1		1
	a*h=		*a(y+z+x)⇔a*h=a*(x+y+z) /:a
2		2

x+y+z=h cnw

Marcin: Dziękuję. 2 już ogarnąłem. Czy ktoś mi podpowie 3?

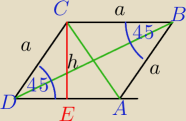
Mila: Dany jest romb ABCD. Odcinek AB = 10, kąt ABC ma miarę 45 stopni. Oblicz długości jego przekątnych i pole tego rombu. ΔDEC : Δprostokątny równoramienny DE=h a=10 h²+h²=10² 2h²=100 h²=50 h=√50=√2*25 h=5√2 P_▱=a*h=10*5√2 P_▱=50√2

	|AC|*|BD|
P▱=
	2

Z tw.cosinusów w ΔABC: |AC|²=8²+8²−2*8*8*cos(45)

	√2
|AC|2=2*64−2*64*
	2

|AC|²=128−64√2 |AC|²=64(2−√2} |AC|=8√2−√2 =========== Porównujemy pola obliczone na dwa sposoby

|AC|*|BD|
	=50√2
2

|AC|*|BD|=100√2 8√2−√2*|BD|=100√2

	100√2
|BD|=
	8√2−√2

=================== P_▱=50√2

Marcin: O dziękuję bardzo.

Mila: