Wykres wartości bezwzględnej
Radek:

Witam mam do narysowania wykres
f(x)=|x
2−4|+3x
Więc zrobiłem to tak
|x
2−4|=−3x Założenie: x≤0
x
2−4=−3x lub x
2−4=3x
x=−4 x=−1
x=1 sprz. x=4 sprz.
Czerwona parabola to: x
2+3x−4
Niebieska parabola to: x
2−3x−4
i teraz jak z tego zrobić |x
2−4|+3x ?
Dziękuje za pomoc
5 paź 18:44
5-latek: |x2−4|=x2−4 dla x nalezy (−oo,−2)U(2,+oo)
w tych przedzialach wzor funkcji jest taki f(x)=x2−4+3x
|x2−4| =−(x2−4)=−x2+4=4−x2 dla x nalezy (−2,2)
wiec w tym przedziale funkcja ma postac f(x)= 4−x2+3x
I teraz rysujesz wykresy tych funkcji ale w tych przdzialach
5 paź 18:54
===:

5 paź 18:55
Radek: 5−latek rozwiązywałeś to na podstawie definicji wartości bezwzględnej?
A tak jak to ja zrobiłem to jest źle ?
5 paź 19:00
===:
tak jak Ty Radek "zrobiłeś" to dzwony z któregoś kościoła ... ale z którego ...
5 paź 19:06
Radek: a co jest źle w mojej metodzie ?
5 paź 19:12
===:
1. Jakim prawem z funkcji robisz równanie

?
a dalej już paaaaaaszło ....
5 paź 19:19
===:
...sam widzisz, że w ten sposób to policzysz miejsca zerowe tej funkcji ... jeśli widzisz −

5 paź 19:24
5-latek: Radek jest chyba zadowolony ze ma wykres

5 paź 19:31
Radek: Czyli za każdym razem jak mam wykres do namalowania to korzystam z definicji ?
5 paź 19:33
Mila:
Radek, to zależy od sytuacji, czasem da się skorzystać z przekształceń wykresu,
f(x)=|x2−4|−3 możesz inaczej
1) rysujesz wykres
y=x2−4
2) symetria względem OX tej części wykresu, co leży pod osią OX i masz
g(x)=|x4−4|
3) translacja wykresu o wektor [0,−3] (3 jednostki w dół) i otrzymujesz wykres f(x)=|x2−4|−3
Spróbuj narysować.
5 paź 19:39
===:
za każdym razem korzystasz z tego co masz pod włosami −

5 paź 19:39
Radek: Tak wyżej ktoś napisał, że jakim prawem z funkcji robię równanie.
Np: x2−3|x|+2
To jak zrobię równanie
−3x=2+x2 lub −3x=−2−x2
i dalej rozwiązuje to to jest źle ?
5 paź 19:47
5-latek:
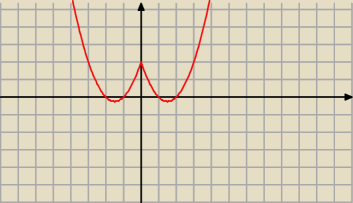
Tak jest zle
Miales napisane dlaczego wiec teraz pytanie do Ciebie . Dlaczego nie stosujes zsie do
wskazowek tylko kombinujesz ?
Maz taka funkcje f(x)=x
2−3|x|+2
Teraz korzystamy z definicji wartosci i mamy |x|=x dla x>=0
wiec nasza funkcja bedziemiala postac w tym przedziale x nalezy <0,+oo) f(x)= x
2−3x+2
Teraz dla x<0 czyli przedzial (−oo,0)
|x|=−x wiec bedzie taka postac f(x)=x
2+3x+2
A teraz Ty napisz jakie dostaniesz postacie funkcji z eswoich rownan
I sprawdz czy dostaniesz taki wykres ze swoich obliczen
I jeszce raz przeczytaj glosno to co jest napisane w poscie 19:39

5 paź 20:00
Radek: Nie no z moich akurat nie wychodzi

No już rozumiem. Dziękuje
5 paź 20:07
5-latek: Czyli jaki wniosek ?
Nie robimy z funkcji rownan>
A powien CI ze takie zadanie bylo na maturze (wiec punkty by poszly w las

5 paź 20:10
Radek: a jak mamy więcej niż jedną wartość bezwzględną w funkcji to wtedy robimy tabelkę i
przedziałami ?
|x+2|−|x|
5 paź 20:22
5-latek: jesli to mabyc funkcja to zapisujemy to tak y=|x+2|+|x| albo np f(x)=|x+2|+|x|
Wtedy widac ze to jest funkcja
Robisz to przedzialami −−tabelki nie robimy No to zrob to zadanie a ja potem sprawdzde
5 paź 20:28
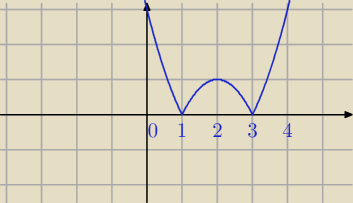
Radek:

Bo ja to robię tak miejsca zerowe
−2 i 0
Tabelka
(−
∞,−2) <−2,0) <0,
∞)
x+2 − + +
x − − +
1. (−
∞,−2)
−x−2+x
f(x)=−2 zielony
2. <−2,0)
x+2+x
f(x)=2x+2 niebieski
3. <0,
∞)
x+2−x
f(x)=2 czerwony
5 paź 20:39
Radek:

Więc ostatecznie wygląda tak
5 paź 20:40
5-latek:

Wykres dobry Ale piszemy tak 1, x∊(−∞,−2) f(x)= 2−x−(−x) to f(x)=2−x+x to f(x)=2 czyli od
razu pod przedzialem piszsemy f(x)= bo to jest funkcja
Popraw zapis pod przedzialami i bedzie OK

5 paź 20:49
Radek: Oki dziękuje. To akurat na studia więc z matury by punkty nie uciekły jedynie z sprawdzianu

5 paź 20:53
5-latek: Na zdrowie

5 paź 20:56
Radek: a jak mamy f(x)=|x2−4x+3| to też korzystamy z własności ?
x2−4x+3≥0 oraz −x2+4x−3<0
7 paź 20:16
Mila:
W tym przypadku rysujesz wykres
g(x)=x2−4x+3
a następnie odbijasz do góry, to co jest pod osią OX.
Otrzymujesz wykres
f(x)=|x2−4x+3|
7 paź 20:26
Radek: Z pierwszego (x2−4x+3≥0) wyszedł mi przedział (−∞,1>u<3,∞)
a z drugiego (−x2+4x−3<0) (−∞,1)u(3,∞) coś chyba jest nie tak
7 paź 20:26
Radek: to tutaj z własności już nie wyjdzie ?
7 paź 20:27
Mila:
Oczywiście, że wyjdzie, ale tak, jak napisałam jest prościej i szybciej.
Widzisz, że pomyliłeś się .
f(x)=(x
2−4x+3 dla x∊(−
∞,1>∪<3,
∞) i rysujesz parabolę na tą dziedziną
(x
2−4x+3≥0)⇔
(x−1)*(x−3)≥0⇔
x≤1 lub x≥3 to masz dobrze
Teraz tak
dla x∊(1,3) ( już nie rozwiązujesz nierówności)
f(x)=−x
2+4x−3 i rysujesz parabolę na tą dziedziną
7 paź 20:40
Radek: No trochę to się komplikuje w pierwszym przypadku rozwiązuje nierówność a w drugim już nie

7 paź 20:55
Mila:
Znasz własności paraboli, jeżeli część leży nad osią OX ( wartości dodatnie funkcji), to reszta
wykresu pod osią i dla argumentów , które zostały, innej możliwości nie ma.
7 paź 21:44
 Witam mam do narysowania wykres
f(x)=|x2−4|+3x
Więc zrobiłem to tak
|x2−4|=−3x Założenie: x≤0
x2−4=−3x lub x2−4=3x
x=−4 x=−1
x=1 sprz. x=4 sprz.
Czerwona parabola to: x2+3x−4
Niebieska parabola to: x2−3x−4
i teraz jak z tego zrobić |x2−4|+3x ?
Dziękuje za pomoc
Witam mam do narysowania wykres
f(x)=|x2−4|+3x
Więc zrobiłem to tak
|x2−4|=−3x Założenie: x≤0
x2−4=−3x lub x2−4=3x
x=−4 x=−1
x=1 sprz. x=4 sprz.
Czerwona parabola to: x2+3x−4
Niebieska parabola to: x2−3x−4
i teraz jak z tego zrobić |x2−4|+3x ?
Dziękuje za pomoc

 ?
a dalej już paaaaaaszło ....
?
a dalej już paaaaaaszło ....



 Tak jest zle
Miales napisane dlaczego wiec teraz pytanie do Ciebie . Dlaczego nie stosujes zsie do
wskazowek tylko kombinujesz ?
Maz taka funkcje f(x)=x2−3|x|+2
Teraz korzystamy z definicji wartosci i mamy |x|=x dla x>=0
wiec nasza funkcja bedziemiala postac w tym przedziale x nalezy <0,+oo) f(x)= x2−3x+2
Teraz dla x<0 czyli przedzial (−oo,0)
|x|=−x wiec bedzie taka postac f(x)=x2+3x+2
A teraz Ty napisz jakie dostaniesz postacie funkcji z eswoich rownan
I sprawdz czy dostaniesz taki wykres ze swoich obliczen
I jeszce raz przeczytaj glosno to co jest napisane w poscie 19:39
Tak jest zle
Miales napisane dlaczego wiec teraz pytanie do Ciebie . Dlaczego nie stosujes zsie do
wskazowek tylko kombinujesz ?
Maz taka funkcje f(x)=x2−3|x|+2
Teraz korzystamy z definicji wartosci i mamy |x|=x dla x>=0
wiec nasza funkcja bedziemiala postac w tym przedziale x nalezy <0,+oo) f(x)= x2−3x+2
Teraz dla x<0 czyli przedzial (−oo,0)
|x|=−x wiec bedzie taka postac f(x)=x2+3x+2
A teraz Ty napisz jakie dostaniesz postacie funkcji z eswoich rownan
I sprawdz czy dostaniesz taki wykres ze swoich obliczen
I jeszce raz przeczytaj glosno to co jest napisane w poscie 19:39 
 No już rozumiem. Dziękuje
No już rozumiem. Dziękuje

 Bo ja to robię tak miejsca zerowe
−2 i 0
Tabelka
(−∞,−2) <−2,0) <0,∞)
x+2 − + +
x − − +
1. (−∞,−2)
−x−2+x
f(x)=−2 zielony
2. <−2,0)
x+2+x
f(x)=2x+2 niebieski
3. <0, ∞)
x+2−x
f(x)=2 czerwony
Bo ja to robię tak miejsca zerowe
−2 i 0
Tabelka
(−∞,−2) <−2,0) <0,∞)
x+2 − + +
x − − +
1. (−∞,−2)
−x−2+x
f(x)=−2 zielony
2. <−2,0)
x+2+x
f(x)=2x+2 niebieski
3. <0, ∞)
x+2−x
f(x)=2 czerwony
 Więc ostatecznie wygląda tak
Więc ostatecznie wygląda tak
 Wykres dobry Ale piszemy tak 1, x∊(−∞,−2) f(x)= 2−x−(−x) to f(x)=2−x+x to f(x)=2 czyli od
razu pod przedzialem piszsemy f(x)= bo to jest funkcja
Popraw zapis pod przedzialami i bedzie OK
Wykres dobry Ale piszemy tak 1, x∊(−∞,−2) f(x)= 2−x−(−x) to f(x)=2−x+x to f(x)=2 czyli od
razu pod przedzialem piszsemy f(x)= bo to jest funkcja
Popraw zapis pod przedzialami i bedzie OK


 Oczywiście, że wyjdzie, ale tak, jak napisałam jest prościej i szybciej.
Widzisz, że pomyliłeś się .
f(x)=(x2−4x+3 dla x∊(−∞,1>∪<3,∞) i rysujesz parabolę na tą dziedziną
(x2−4x+3≥0)⇔
(x−1)*(x−3)≥0⇔
x≤1 lub x≥3 to masz dobrze
Teraz tak
dla x∊(1,3) ( już nie rozwiązujesz nierówności)
f(x)=−x2+4x−3 i rysujesz parabolę na tą dziedziną
Oczywiście, że wyjdzie, ale tak, jak napisałam jest prościej i szybciej.
Widzisz, że pomyliłeś się .
f(x)=(x2−4x+3 dla x∊(−∞,1>∪<3,∞) i rysujesz parabolę na tą dziedziną
(x2−4x+3≥0)⇔
(x−1)*(x−3)≥0⇔
x≤1 lub x≥3 to masz dobrze
Teraz tak
dla x∊(1,3) ( już nie rozwiązujesz nierówności)
f(x)=−x2+4x−3 i rysujesz parabolę na tą dziedziną
