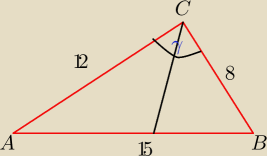
Dwa zadania - planimetria trq: 1. Dany jest trójkąt ABC o bokach 8, 12, 15. Oblicz: a) długości odcinków na które dwusieczna BCA dzieli bok AB b) długość odcinka dwusiecznej kąta BCA zawartego w tym trójkącie 2. Przekątne trapezu ABCD o podstawach AB i CD przecinają się w punkcie P. Pola ABP i CDP są odpowiednio równe 16 i 9. Oblicz pole BCP.

	γ
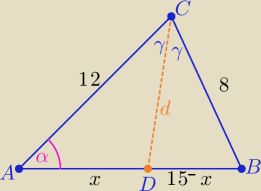
Rysunek do zadania 1− kąty przy wierzchołku C to		(nie mogłem ich zaznaczyć)
	2

trq: ponawiam

PW: Wskazówka:

	|AD|		|AC|
		=
	γ   sin   2		sinδ

− twierdzenie sinusów zastosowane w ΔADC.

	|BD|		|BC|
		=
	γ   sin   2		sin(180°−δ)

gdzie D − punkt, wspólny dwusiecznej i podstawy, a δ i 180°−δ − kąty o wierzchołku D. Kiedy to podzielisz stronami przez siebie, otrzymasz tzw. twierdzenie o dwusiecznej.

trq: Okej. Rozwiązałem równanie i wyszło BD=6 AD=9. Dzięki wielkie za pomoc. Jakieś pomysły co do drugiego zadania?

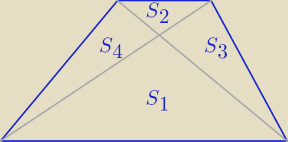Eta: S₃=S₄ =√S₁*S₂ = ...... = 12

Eta:

	12		8
1/ a) z tw. o dwusiecznej		=		⇒ x= 9
	x		15−x

|AD|=9 , |DB|= 15−9=6

	122+152−82
b)z tw. kosinusów w ΔABC cosα=		=......
	2*12*15

z tw. kosinusów w ΔADC d²= 12²+9²−2*12*9*cosα =..... ⇒ d=....

Eta: zad2/ 2 sposób

	S1		4
ΔABP ∼ ΔCPD w skali k>0 ⇒		= k2 ⇒ k=
	S2		3

P₃=P₄= k*P₂= ...... =12