kombinatoryka zadanie: Mamy do dyspozycji n klatek ustawionych szeregowo, chcemy rozmieścić k nierozróżnialnych lwów tak, by żadne lwy nie sąsiadowały ze sobą. Niech g(n,k) bedzie liczbą sposobów rozmieszczania lwów. Udowodnic ze: a) g(6, 3)=4 b) g(2k,k)=k+1 c) g(n,k)=g(n−2, k−1)+g(n−1,k), k=2, 3, ... Moglbym poprosic o pomoc?

daras: g(6,3) = 2

daras: g(6,3) = 2

Kacper: Głupie było to zadanie Gdzie studiujesz?

Kacper: daras dlaczego sądzisz, że g(6,3)=2?

PW: (0,1,0,1,0,1) (1,0,1,0,1,0) (1,0,0,1,0,1) (1,0,1,0 0,1) − nie pogryzą się.

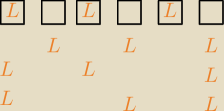
Mila: g(6,3)=4

daras: w wyższej szkole cyrkowej