zespolone
razor:
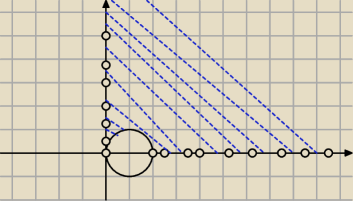
Określ geometrycznie zbiór A punktów płaszczyzny zespolonej
| | π | |
A = {z∊C: 0<argz< |
| , |z−i| ≥ 1} |
| | 2 | |
|z−i| ≥ 1
|x+(y−1)i| ≥ 1
x
2+(y−1)
2 ≥ 1
warunek z argz to wg mnie znaczy że ten obszar leży w I ćwiartce układu wsp.
Czy to jest dobrze?

5 paź 14:17
mto: a nie powinno być tak ?
|x+(y−1)i| ≥ 1 / 2
x2+(y−1)2i2 ≥1
x2−(y−1)2 ≥1
?
5 paź 14:35
Godzio:
|z − z0| = r ≥ 0
Okrąg o środku w z0 i promieniu r (r = 0 − punkt)
Więc w przypadku |z − i| ≥ 1 mamy okrąg o środku (0,1) i promieniu 1 + wszystko poza nim
Zadanie ok.
5 paź 14:41
razor:
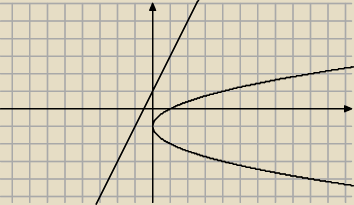
jeszcze jedno:
|z+i| > rez+1
|x+(y+1)i| > x+1 |
2 zał. x ≥ −1
x
2+(y+1)
2 > x
2+2x+1
(y+1)
2 > 2x+1
jak narysuje to tak, to rozwiązaniem jest zbiór pusty...
5 paź 14:55
razor:
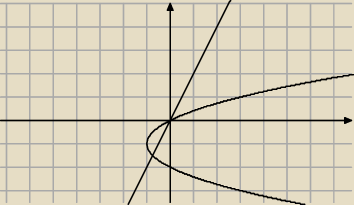
y
2+2y+1>2x+1
y
2+2y>2x
a w ten sposób nie, i wg odpowiedzi tak ma wyjść
gdzie jest błąd?
5 paź 14:55
Godzio:
Przypadek x ≥ − 1 rozpatrzyłeś, a co dla x < −1?
5 paź 15:00
razor: dla x < −1 nierówność jest zawsze spełniona
5 paź 15:12
Godzio:
No to zbiorem rozwiązań jest {(x,y) : x < −1 i y ∊ R} albo równoważnie {z : Rez < −1}
5 paź 15:13
razor: odpowiedź jest taka: część płaszczyzny ograniczona parabolą o równaniu 2x = y2+2y (2x <
y2+2y)
5 paź 15:17
Godzio:
Czyli to jest ten skrawek między 2x, a parabolą? Zaraz pomyślę...
5 paź 15:23
razor: podbijam
5 paź 16:59
Kacper:
Mnie wychodzi coś takiego:
x<−
12 i y∊R
lub x>−
12 i (y>
√2x+1−1 lub y<−2
√2x+1−1)
Jakoś tak

5 paź 18:02
Mila:
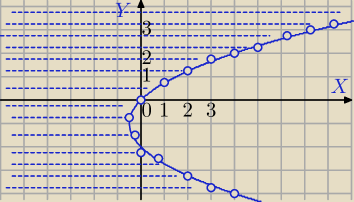
(y+1)
2 > 2x+1
(y+1)
2−1>2x /:2
to jest parabola "obrócona" − poczytaj o paraboli ( znajdę materiał, to dam linka)
Ramiona skierowane na prawo.
Szukany obszar to punkty na lewo od paraboli.
5 paź 20:23
5 paź 20:28
 Określ geometrycznie zbiór A punktów płaszczyzny zespolonej
Określ geometrycznie zbiór A punktów płaszczyzny zespolonej

 jeszcze jedno:
|z+i| > rez+1
|x+(y+1)i| > x+1 |2 zał. x ≥ −1
x2+(y+1)2 > x2+2x+1
(y+1)2 > 2x+1
jak narysuje to tak, to rozwiązaniem jest zbiór pusty...
jeszcze jedno:
|z+i| > rez+1
|x+(y+1)i| > x+1 |2 zał. x ≥ −1
x2+(y+1)2 > x2+2x+1
(y+1)2 > 2x+1
jak narysuje to tak, to rozwiązaniem jest zbiór pusty...
 y2+2y+1>2x+1
y2+2y>2x
a w ten sposób nie, i wg odpowiedzi tak ma wyjść
gdzie jest błąd?
y2+2y+1>2x+1
y2+2y>2x
a w ten sposób nie, i wg odpowiedzi tak ma wyjść
gdzie jest błąd?

 (y+1)2 > 2x+1
(y+1)2−1>2x /:2
(y+1)2 > 2x+1
(y+1)2−1>2x /:2