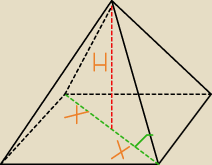
 Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do
płaszczyzny podstawy pd kątem 40∘. Oblicz objętość tego ostrosłupa.
Powie mi ktoś, co zrobiłem źle?
H=8
2x = przekątna
tg40*= Hx
0,84 = 8x
84100 = 8x ( na krzyż )
x = 9,52 , 2x = 19,04 (przekątna)
długość boku a ( 2x = a √2 ) −> ( 952√2 )
Do wzoru V = 1/3 * 952 √2 * 8 ~ 2538,66 √2 ...
Prawidłowa odpowiedź to 484,79... Nie jestem dobry z matmy także byłbym wdzięczny jakby ktoś
wskazał mi mój błąd...
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do
płaszczyzny podstawy pd kątem 40∘. Oblicz objętość tego ostrosłupa.
Powie mi ktoś, co zrobiłem źle?
H=8
2x = przekątna
tg40*= Hx
0,84 = 8x
84100 = 8x ( na krzyż )
x = 9,52 , 2x = 19,04 (przekątna)
długość boku a ( 2x = a √2 ) −> ( 952√2 )
Do wzoru V = 1/3 * 952 √2 * 8 ~ 2538,66 √2 ...
Prawidłowa odpowiedź to 484,79... Nie jestem dobry z matmy także byłbym wdzięczny jakby ktoś
wskazał mi mój błąd...
| H | 8 | |||
tg 40o = | = | |||
| x | x |
| 8 | ||
0,8391 = | ||
| x |
| 1 | 1 | |||
V = | Pp *H ≈ | *181,794*8 ≈ 484,78 | ||
| 3 | 3 |