Przedstaw w postaci kanonicznej Zuza: Przedstaw w postaci kanonicznej trójmian kwadratowy, następnie ogranicz dziedzinę do takiego przedziału, w którym dana funkcja jest różnowartościowa i wyznacz wzór oraz narysuj funkcję odwrotną: Prosze moze ktos ten jeden przyklad caly rozwiazac dla przykladu a) y= x² + 2x + 1

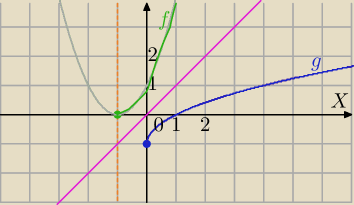
Mila: f(x)=(x+1)²+0 p=−1, q=0 dla x≥−1 funkcja jest różnowartościowa Wybieram D=<−1,∞) y=(x+1)² x+1=√y x=√y−1 Zamieniam zmienne: g(x)=√x−1 wzór funkcji odwrotnej do f(x) =(x+1)² i x∊<−1,∞) Wykresy są symetryczne względem prostej y=x

Zuza: Jak sie rysuje funkcje odwrotną ? z czego wynika to jak będzie przebiegać jak na tym przykładzie ze przechodzi przez punkt (1,0) bo obliczyłam sobie inny przykład y=−x²+4x+1 i wychodzi mi z tego y=√x−5+2 i jak ta funkcje odwrócona narysować ?

daras: a w podręczniku tego nie ma ?

Zuza: Bedzie ktos tak pomocny:(

Mila: Źle, wyznaczyłaś ten wzór. Podstawiasz sobie kilka argumentów do wzoru i liczysz wartości, jeśli nie uczono Cię przekształceń wykresów . y=√x−1 rysujesz tak 1) rysujesz wykres funkcji y=√x, D=<0,∞), sporządzasz tabelkę i szkicujesz. 2) następnie przesuwasz wykres o jedną jednostkę w dół , otrzymujesz wykres f(x)=√x−1 i dlatego f(0)=−1 wykresy g(x)=√x−5+2 1) wykres y=√x 2) translacja o wektor [5,2] i otrzymujesz wykres funkcji g(x)=√x−5+2

Saizou : funkcja odwrotna jest zawsze symetryczna względem prostej y=x od funkcji wyjściowej

Mila: f(x)=−x²+4x+1

	−4
xw=		=2
	−2

f(2)=5 f(x)=−(x−2)²+5 postać kanoniczna x≥2 y=−(x−2)²+5 y−5=−(x−2)² /*(−1) 5−y=(x−2)² x−2=√5−y dla y≤5 x=2+√5−y Zamiana zmiennych: y=2+√5−x Narysuj prostą y=x i odbij przez symetrię jedną gałązkę paraboli.

Mila: No to niepotrzebnie to pisałam?

Zuza: Po co mnożysz przez −1 ====> y−5=−(x−2)² /*(−1)

Mila: Taki zapis : y−5=−(x−2)² jest równoważny zapisowi y−5=(−1)*(x−2)² wyznaczam (x−2)² (x−2)²=(y−5)*(−1) (x−2)²=5−y