Rozwiąż nierówność
broken04: |1−x|−|x|≥3
Czy takie zadanie dam rady rozwiązać siatką znaków? Proszę o pomoc
4 paź 12:35
5-latek: Na jaka cholere CI tu potrzebna siatka znakow
Siatka znakow jest owszsem dobra ale do zwyklych nierownosci .
Zapytaj jeszce o to swojego nauczyciela
4 paź 13:26
broken04: to jak takie dziadostwo rozwiązać? Umiem trudne cholerstwa trzaskać a tego nie wiem jak
ruszyć...
4 paź 13:30
5-latek: Pewnie bedzie najwieksza trudnosc z |x| ? Tak?
Zapewne wiesz ze |x|=x gdy x>=0 i |x| =−x gdy x<0
Zobacz jesli trudne trzaskasz to bedziesz mial takie przedzialy
1 x nalezy (−oo,0>
2przedzial x nalezy (0,1>
3 przedzial (1,oo)
4 paź 13:37
broken04: dzięki
4 paź 13:47
Kacper:
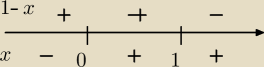
Ja polecam uczniom robienie czegoś takiego.
4 paź 14:29
Lukas:
Czemu tak polecasz ?
4 paź 14:31
Kacper: Żeby nie mylili się kiedy mają zmienić znak, a kiedy nie. Na początku określają kiedy dodatnie
i kiedy ujemne i potem tylko podstawiają.
4 paź 14:36
Lukas:
ale to nie działa jeśli w module jest x
2+...

4 paź 14:36
ICSP: Zadanie na myślenie, a nie na rozpatrywanie przypadków. Jeżeli osoba która dobrze opanowała
definicję wartości bezwzględnej spojrzy na powyższą nierówność to zapewne od razu powie
równanie sprzeczne.
4 paź 14:40
Kacper: ICSP nie wiem czy w mojej szkole znalazł by się uczeń, który to widzi.
4 paź 14:42
ICSP: Znalazłoby się nawet kilku

4 paź 14:44
Kacper: ICSP nie byłeś dawno w szkole

4 paź 14:45
Lidka:
II sposób
|1−x|−|x|≥3 /+|x|
|1−x|≥|x|+3 obie strony nieujemne, to podnosimy do kwadratu
(1−x)2≥x2+2|x|+9
1−2x+x2≥x2+2|x|+3
1−2x≥2|x|+3
−2x≥2|x|+2 /:(2)
−x≥|x|+2
jeśli nie widzisz sprzeczności, to dalej tak:
1) |x|=x dla x≥0
−x≥x+2
−2x≥2
x≤−1 zbiór nie spełnia warunku x≥0, brak rozwiązań
2) |x|=−x dla x<0
−x≥−x+2⇔
0≥2 sprzeczność.
4 paź 15:09
ICSP: |x − 1| − |x| ≤ | |x−1| − |x|| ≤ |x − 1 − x| = 1 < 3 − dla dowolnego x
Równanie jest zatem sprzeczne
4 paź 15:14
Pat:
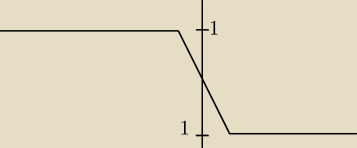
Witam, mam pytanie.
Narysowałem na kalkulatorze tą funkcję |1−x|−|x|=y i faktycznie równanie jest sprzeczne.
Standardowo tak rozwiązywałem tą nierówność:
Kacper narysował przedziały i określił kiedy wyrażenia są ujemne i dodatnie, więc:
1. dla x∊(−
∞,0)
1−x−x≥3
1≥3
sprzeczność
x∊Ø
2.dla x∊<0,1)
1−x−x≥3
x≤1 i D
x∊<0,1)
3.dla x∊<1,
∞)
x−1−x≥3
−1≥3
sprzeczność
x∊Ø
Wynik to suma rozwiązań z poszczególnych przypadków, więc"
x∊Ø oraz x∊<0,1) oraz x∊Ø
Na maturze napisałbym pewnie, że rozwiązaniem jest ten przedział: x∊<0,1).
Moje pytanie jest następujące. Czyli jak pojawi się w jednym rozwiązaniu "sprzeczność" to cała
nierówność będzie sprzeczna?
29 sty 15:26
Szkolniak: Błąd w 2) 1−x−x≥3 ⇔ −2x≥2 ⇔x≤−1
29 sty 16:15
Pat: Faktycznie, czyli byłoby:
2. x≤−1i D: x∊<0,1)
x∊Ø
Odpowiedź: brak rozwiązań.
A gdyby hipotetycznie w 2. wyszedł jakiś przedział jako odpowiedź, a w 1. i 3. była sprzeczność
to finalna odpowiedź jest tym przedziałem z 2.

(Jeżeli oczywiście mamy sumę przedziałów a nie
część wspólną przypadków)
29 sty 16:53
Szkolniak: Tak jak mówisz
29 sty 22:13
a@b:
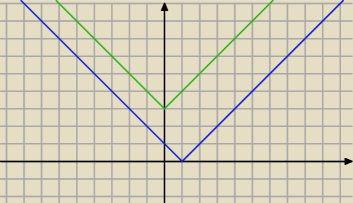
|1−x|−|x|≥3
|x−1|≥|x|+3
y=|x−1| ,
y=|x|+3
taka nierówność jest sprzeczna
x∊∅
30 sty 00:14
 Ja polecam uczniom robienie czegoś takiego.
Ja polecam uczniom robienie czegoś takiego.



 Witam, mam pytanie.
Narysowałem na kalkulatorze tą funkcję |1−x|−|x|=y i faktycznie równanie jest sprzeczne.
Standardowo tak rozwiązywałem tą nierówność:
Kacper narysował przedziały i określił kiedy wyrażenia są ujemne i dodatnie, więc:
1. dla x∊(−∞,0)
1−x−x≥3
1≥3
sprzeczność
x∊Ø
2.dla x∊<0,1)
1−x−x≥3
x≤1 i D
x∊<0,1)
3.dla x∊<1,∞)
x−1−x≥3
−1≥3
sprzeczność
x∊Ø
Wynik to suma rozwiązań z poszczególnych przypadków, więc"
x∊Ø oraz x∊<0,1) oraz x∊Ø
Na maturze napisałbym pewnie, że rozwiązaniem jest ten przedział: x∊<0,1).
Moje pytanie jest następujące. Czyli jak pojawi się w jednym rozwiązaniu "sprzeczność" to cała
nierówność będzie sprzeczna?
Witam, mam pytanie.
Narysowałem na kalkulatorze tą funkcję |1−x|−|x|=y i faktycznie równanie jest sprzeczne.
Standardowo tak rozwiązywałem tą nierówność:
Kacper narysował przedziały i określił kiedy wyrażenia są ujemne i dodatnie, więc:
1. dla x∊(−∞,0)
1−x−x≥3
1≥3
sprzeczność
x∊Ø
2.dla x∊<0,1)
1−x−x≥3
x≤1 i D
x∊<0,1)
3.dla x∊<1,∞)
x−1−x≥3
−1≥3
sprzeczność
x∊Ø
Wynik to suma rozwiązań z poszczególnych przypadków, więc"
x∊Ø oraz x∊<0,1) oraz x∊Ø
Na maturze napisałbym pewnie, że rozwiązaniem jest ten przedział: x∊<0,1).
Moje pytanie jest następujące. Czyli jak pojawi się w jednym rozwiązaniu "sprzeczność" to cała
nierówność będzie sprzeczna?
 (Jeżeli oczywiście mamy sumę przedziałów a nie
część wspólną przypadków)
(Jeżeli oczywiście mamy sumę przedziałów a nie
część wspólną przypadków)
 |1−x|−|x|≥3
|x−1|≥|x|+3
y=|x−1| , y=|x|+3
taka nierówność jest sprzeczna
x∊∅
|1−x|−|x|≥3
|x−1|≥|x|+3
y=|x−1| , y=|x|+3
taka nierówność jest sprzeczna
x∊∅