funkcja dyzio: Zilustruj zbiór wszystkich punktów płaszczyzny, których współrzędne (x,y) spełniają równanie. 2|x| − |y + 2| = 1 Domyślam się, że trzeba będzie to rozwiązać siatką znaków, ale jak ? Osobną dla x i y ?

dyzio: jakaś wskazówka ?

Bogdan: |y + 2| = 2|x| − 1 dla y < −2: y + 2 = −2|x| + 1 ⇒ y = −2|x| − 1 dla x ≥ −2: y + 2 = 2|x| − 1 ⇒ ....

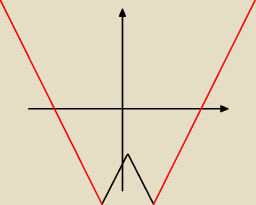
dyzio: że niby coś takiego ma wyjść ?

Bogdan: Mała poprawka, w ostatnim wierszu u mnie ma być: dla y ≥ −2 (a nie dla x ≥ −2)

Bogdan: Twój rysunek nie jest dobry

dyzio: nie rozumiem jednego dlaczego na osi x D∊(−∞; −0,5)∪(0,5; +∞) ? Po narysowaniu

Kacper: D=R

dyzio: Tak ma mniej więcej wyglądać ten wykres ? Sorki ale nie umiem szkicować

dyzio:

Kacper:

dyzio: dzięki za pomoc

Bogdan: Te rysunki nie są dobre

Kacper: Rzeczywiście. Nie zauważyłem przesunięcia

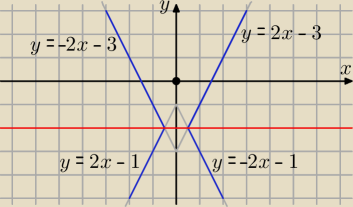
Bogdan: Pełne rozwiązanie: 2|x| − |y + 2| = 1 dla x ≥ 0 i y ≥ −2: 2x − y − 2 = 1 ⇒ y = 2x − 3 dla x < 0 i y ≥ −2: −2x − y − 2 = 1 ⇒ y = −2x − 3 dla x < 0 i y < −2: −2x + y + 2 = 1 ⇒ y = 2x − 1 dla x ≥ 0 i y < −2: 2x + y + 2 = 1 ⇒ y = −2x − 1