Analiza Piotr 10: Udowodnij, że log₂ 3 jest liczbą niewymierną Dowód nie wprost, zakładam, że jest liczbą wymierną

	p
log23=		, gdzie p∊Z ⋀ q∊CN
	q

q*log₂3 = p log₂3^q=p 2^p = 3^q Lewa strona zawsze jest parzysta, zaś prawa jest nieparzysta. Co prowadzi do sprzeczności, L_s≠P_s. Zatem log₂3 jest liczbą niewymierną OK?

Piotr 10:

	π
To samo z cos
	8

Skorzystałem ze znanego wzoru nam i wyszło przymując, że kąt alfa leży w I ćw, układu kartezjańskiego

	π		√2+√2
cos		=
	8		2

Kacper:

Piotr 10: Mam pytanie Zacząłem dzisiaj analizę matematyczną. Robić zadania po kolei ze Skoczylasa ? Dobrze robię ? Chodzi o dział zbiór liczb rzeczywistych. Oczywiście takich dowodów na studiach nie miałem. Może takie coś pojawić się na jakimś sprawdzianie czy coś ? Jak to jest ?

Kacper: Przede wszystkim rób to, co wymaga osoba prowadząca zajęcia. Nie wiem co dokładnie masz na tych wykładach i ćwiczeniach.

Piotr 10: Ok. Miałem funkcje cyklometryczne czy jakieś tam. Dziwne to trochę, ale na razie to skończe

Kacper: Zapewne arctg, arccos, arcsin, arcctg?

Piotr 10: arc sin (sinx) czarna magia. Nie potrafiłem w ogóle zrozumieć prowadzącego ćwiczenia z analizy

Kacper: arcsin(x) tak?

Piotr 10: Nie arcsin( sinx) − to narysować sinus hiperboliczny i cosinus.

Piotr 10: Mam nadzieję, że Skoczylas powinien wystarczyć chociaż by na 3 plus jakaś własna rozkmina

Kacper: y=sin(x) x=arcsin(y)=arcsin(sin(x)) Tylko należy pamiętać, że odwracamy funkcje w przedziałach.

Mila: Piotrze W Skoczylasie jest dokładnie wyjaśniony ten wykres, pisałam to , ale coś mi się komputer zbuntował i wszystko zniknęło po komunikacie "niedobrze." Czytaj i zadaj pytanie, gdzie masz wątpliwości.

Piotr 10: Na razie to czytam kresy górne zbiorów i dolne. Dziś 4h analizy, jest co robić. Oczywiście na wykładach co innego a na ćwiczeniach też co innego. Ale przywykłem Będę pisać jak coś

Piotr 10: Mila jakoś nie mogę znależć wyjaśnienia tego wykresu funkcji

Mila: Funkcje cyklometryczne. Jutro Ci mogę napisać, bo dziś komputer coś mi fiksuje z wykresami.

Piotr 10: Tylko są podstawowe funkcje, czyli arcctg x itd Nie ma arccos(cosx)

Piotr 10: Ok

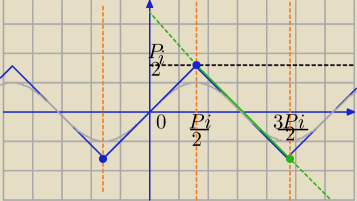
Mila: f(x)=arcsin(sin(x)) D_f=<−1,1>

	π		3π
Sin(x) jest funkcją okresową , T=2π, rozważymy wykres w przedziale <−		,		>.
	2		2

Funkcja odwrotna istnieje dla funkcji różnowartościowej.

	π		π
Dla x∊<−		,		>
	2		2

sin(x) jest funkcją różnowartościową Zw=<−1,1>, co pokrywa się z dziedziną y=arcsin(t)

	π		π
Wtedy f(x)=x dla x∊<−		,		> z definicji funkcji odwrotnej.
	2		2

	π		3π
W przedziale (		,		> argumenty są przesunięte o π w stosunku do poprzedniego
	2		2

przypadku. Wartości funkcji maleją od 1 do (−1).

	π		π
x=π+u, gdzie u∊(−		,		> stąd u=x−π
	2		2

f(x)=arcsin(sinx))=arcsin(sin(π+u))=arcsin(−sinu))=−arcsin(sin(u))=−u=−(x−π)=−x+π Podsumowanie :

	π		π
f(x)=x dla x∊<−		,		>
	2		2

	π		3π
f(x)=−x+π dla x∊(		,		>
	2		2

Mila: Jest Trivial, Godzio,ICSP, to na pewno spojrzą i coś lepiej wyjaśnią, są na bieżąco z materiałem.

Piotr 10: Ok, dziękuję

Piotr 10: Znaleźć

	n−1
sup {		: n∊N }
	n

n−1		1
	= 1 −		i n∊N
n		n

supremum czyli największy element zbioru A supA = 1

Ajtek: A przypadkiem nie 0? dla n=1 masz 1−1=0. Ręki sobie nie dam jednak uciąć. Cześć Piotr 10 .

Piotr 10: Witaj, nie wiem właśnie

WueR: Element najmniejszy i supremum to dwa rozne pojecia.

WueR: Element najwiekszy*

Piotr 10: :(. Pomożesz, bo sobie nie daje rady ?

WueR: Supremum w tym przypadku bedzie wlasnie 1. Ale wlasnie wbrew temu co wczesniej powiedziales

	n−1
"supremum czyli najwiekszy element zbioru A" − no bo przeciez 1∉{		:n∊N}, czyz nie?
	n

Piotr 10: No tak. A możesz coś więcej napisać o supremum i inf ? Bo ciężko mi idzie

WueR: No to zerknij na definicje. Supremum to najmniejsze ograniczenie gorne danego zbioru. A jak nie wiesz, co to ograniczenie, to znowu zerknij na jego definicje. Infimum analogicznie.

Piotr 10: Ok. Już lepiej

	n+1
inf {		, n∊N}
	n

Też 1?

WueR:

Piotr 10: A jak z tymi wykresami funkcji arc sin(sinx). Nie potrafie tego zrozumiec

WueR: Tzn. czego dokladnie nie potrafisz zrozumiec?

Piotr 10: Wieczorem napiszę, teraz definicje granicy ciągu

Piotr 10: Mila w Skoczylasie jest napisane, że dziedziną funkcji f(x)= arcsin(sinx) jest R, dlaczego

#banasz: arcsin x −> −1 ≤ x ≤ 1 arcsin(sin x) −> −1 ≤ sin x ≤ 1 −> dla x ∊ R

Piotr 10: OK. Thx

Mila: Tak, mój zapis D dotyczył funkcji y=arcsin(t), to miałam na myśli, komputer mi coś fiksował i to była kolejna wersja , więc z usterką, Banasz ładnie wyjaśnił.

Piotr 10: Szczerze to nie rozumiem tego zadania. Za trudny przykład dla mnie.

Mila: Przeczytaj kilka razy, patrz na wykres. Ważna jest dziedzina i zbiór wartości funkcji.

AAAAA: Piotr 10, jak chcesz to tutaj jest to bardzo dokładnie wytłumaczone: http://wyrownawcze.mini.pw.edu.pl/attachments/074_zad_10_dodatkowy.pdf

Piotr 10: Popytam ludzi na uczelni, bo nadal tego nie potrafię . Dzięki za chęci pomocy