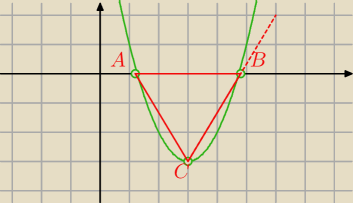
Geometria na układzie - sprawdzenie Mariusz Pudzianowski: Wierzchołki Trójkąta równobocznego leżą na wykresie paraboli y=x²−6x+6 Punkt C jest wierzchołkiem paraboli a odcinek AB jest równoległy do OX. Narysuj układ współ i wyznacz wierzhołki. I teraz mam pytanie czy można zrobić tak że C=(3,−3) xb+xa=6 − składowa xc musi być środkiem odcinka AB xb−xa=3 − jak się odejmie tą dłg odcinka od początku układu współ do xa od dłg odcinka od początku uw do xb to musi być 3 I wtedy B=(9/2 ; 3/4) A = (3/2 ; 3/4) Czy to wystarczy, znaczy się czy te warunki zapewniają że ABC bd równoboczny czy trzeba jeszcze udowadniać z wzoru na dłg odcinka ża AB=BC=AC ?

Tadeusz: ... przeczytaj o co pytają? −

Mariusz Pudzianowski: Przecież wyznaczyłem tylko się zastanawiam czy te dwa warunki które dałem wymuszają żę bęzie zawsze równoboczny, bo przecież w równoramiennym składowa xc też byłaby środkiem odcinka

Tadeusz: ... zrównałeś wysokość trójkąta z jego bokiem

Mariusz Pudzianowski: No to A(xa,ya=f(xa)) B(xb,yb=ya) xa+xb=6 xa−xb=(xb+xa)−2xa=6−2xa √(6−2xa)² = √(xa−3)²+(f(x)+3)² (6−2xa)²=(xa−3)² + (f(x)+3)² 36 − 24xa + 4xa² = xa² − 6xa + 9 + (f(x))² + 6f(x) + 9 36−24xa + 4xa² = xa² − 6xa + 9 + xa⁴ − 12xa³ + 48xa² − 72xa + 36 + 6xa² − 36xa +36 + 9 4xa² − 24xa + 36 = xa⁴−12xa³ + 55xa² − 144xa − 54 xa⁴−12xa³ + 51xa² − 120xa + 90 = 0 I jak odnaleźć pierwiastek bez wolfram alpha ?

Mariusz Pudzianowski: ktoś coś ? Tadeusz ?

Tadeusz: ...a może tak... Skoro trójkąt równoboczny to jego jeden z boków zawiera się w prostej o współczynniku a=√3 Dodatkowo wiesz, że przechodzi na przez C=(3, −3) Teraz poszukaj punktu przecięcia tej prostej z parabolą

Tadeusz: czyli: y=√3x−3−3√3 √3x−3−3√3=x²−6x+6 ⇒ x²−x(6+√3)+9+3√3=0 Δ=36+12√3+3−36−12√3 √Δ=√3 x₁=x_c=3 x₂=x_B=3+√3 y_B=0

Mariusz Pudzianowski: Wielkie dzięki

...: −