Trójkąt ABC truskawka: W trójkącie ABC bok AC jest równy 3√2, a bok AB jest o 4 większy od boku CB. a) oblicz obwód tego trójkąta b) oblicz promień okręgu opisanego c) oblicz sinus β Proszę o pomoc, zgubiłam się trochę

sushi_gg6397228: a ten trojkat jakiś szczególny jest ?

truskawka: nie, nie, nic nie było właśnie podane

sushi_gg6397228: coś musi być; inaczej sie nie policzy

truskawka: a co np?

truskawka: a tak.. jeszcze był kąt, przepraszam, nie zauważyłam... ∡ACB=135 stopni

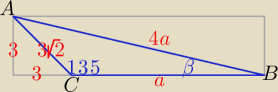
Bogdan: Np. w ten sposób: (a + 3)² + 9 = 16a² ⇒ a = ...

truskawka: jest o 4 większy, nie 4x większy. a nie dałoby się z twierdzenia cosinusów?

Mila: Da się. Zapisz i oblicz sprawdzę. |AB|=a+4

	√2
cos(135o)=−
	2

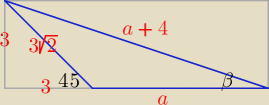
Bogdan: No to wystarczyło zamiast 4a wziąć 4+a i obliczyć a w ten sposób: (a + 3)² + 9 = (a² + 4)² ⇒ a² + 6a + 18 = a² + 8a + 16 ⇒ 2a = 2 ⇒ a = 1

	3
sinβ =		= ...
	a + 4

	3√2
R =		, R − długość promienia okręgu opisanego
	2sinβ

Bogdan: poprawiam: (a + 3)² + 9 = (a + 4)² ⇒ ....

truskawka: wyszło mi a=1

truskawka: (a+4)² =a²+(3√2)² − 2*(3√2) * a * − cos 45 stopni a² + 8a+16=a²+18+6a 8a+16=18+6a 2a=2 a=1