funkcje Blue: Jeśli m1 i m2 są różnymi wartościami parametru m, dla których równanie −2^|x| +4 = m² ma jedno rozwiązanie , to suma m1²+m2² jest równa..... ile? Narysowałam to i mi wychodzi, że jedno rozwiązanie jest tylko dla jednego m, więc nie wiem, o co tutaj chodzi....

Blue: Pomożecie?

PW: 2^|x| przyjmuje wartości z przedziału [1,∞) i jest parzysta (wykres symetryczny względem osi OY). Funkcja g(x) = − 2^|x| jest także parzysta, ale przyjmuje wartości z przedziału (−∞, −1]. Funkcja f(x) = g(x) + 4 przyjmuje zatem wartości z przedziału (−∞, −3] i jest parzysta. Już widać, dla jakich m jest tylko jedno rozwiązanie?

Blue: ten ostatni przedział, który napisałeś nie powinien wyglądać tak: (−∞,3>

Blue: Co tak dziś zamulacie ? Tyko bez obrazy i śpieszy mi się, więc sorki za niecierpliwość

PW: Jak zwykle.

Kacper: "i spieszy mi się" − płacisz za pomoc, że tak wymagasz

PW: Kacper, gdyby ktoś nawet chciał mi płacić i tak się zachowywał, to nie dokończylibyśmy nawet pierwszej lekcji. To jest moja ostatnia porada dla Blue.

Blue: oj, no przecież napisałam, żebyście się nie obrażali Nie bądźcie tacy wrażliwi

Blue: Czy mógłby ktoś wytłumaczyć, dlaczego zbiór wartości tej funkcji nie wygląda tak: (−∞,3>?

Blue: PW dzięki Ci za pomoc, jednak nie rozumiem tego ostatniego wniosku i tylko proszę o wytłumaczenie, nie wiem, o co się tak urażasz Kacper − nawet Ty przeciwko mnie?:(

Blue: Nikt nie pomoże

===:

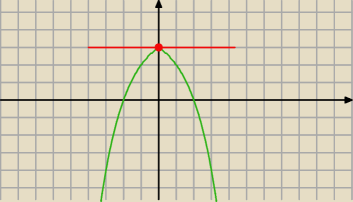
Blue: No czyli dobrze mam Taki właśnie mam rysunek do tego. Ale gdzie tutaj są dwie wartości m , dla których rozwiązanie jest jedno? Bo ja widzę tylko jedną taką wartość parametru m...

Kacper: Suma jest równa 6

===: ... Kobito ... − Ta czerwona krecha to m² m²=3 czyli m₁=−√3 m₂=√3

Blue: a więc to o to chodziło Dziękuję za pomoc

===: ... szkoda głowy −