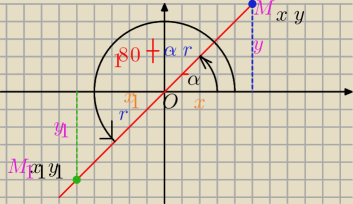
 Jak sa polozone wzgledem siebie koncowe ramiona kątow α i 180+α? Przyjalem ze α=45 to
180+α=225 (tak dla potrzeb rysunku
Nie wiem jak to nazwac ale powiedzmy ze tak .
Koncowe ramiona kątow α i 180+α leza naprzeciwko siebie
Z tego rysunku mam wyprowadzic wzory na sin(180+α) cos(180+α), tg(180+α) i ctg(180+α)
x1=−x y1=−y i OM=OM1=r
Jak sa polozone wzgledem siebie koncowe ramiona kątow α i 180+α? Przyjalem ze α=45 to
180+α=225 (tak dla potrzeb rysunku
Nie wiem jak to nazwac ale powiedzmy ze tak .
Koncowe ramiona kątow α i 180+α leza naprzeciwko siebie
Z tego rysunku mam wyprowadzic wzory na sin(180+α) cos(180+α), tg(180+α) i ctg(180+α)
x1=−x y1=−y i OM=OM1=r
| y1 | −y | |||
sin(180+α)= | = | = −sinα | ||
| r | r |
| x1 | −x | |||
cos(180+α)= | = | = −cosα | ||
| r | r |
| y1 | −y | |||
Teraz jesli x≠0 i x1≠0 to tg(180+α)= | = | =tgα | ||
| x1 | −x |
| x1 | −x | |||
Jezeli y≠0 i y1≠0 to ctg(180+α)= | = | =ctgα | ||
| y1 | −y |